Es ist ein hübsches Spiel für geduldige Kinder: Auf einer Holzplatte ist ein Kreis aufgezeichnet, und auf dem Umfang dieses Kreises sind in gleichmäßigen Abständen p – 1 Nägel eingeschlagen, wobei p in der Größenordnung von einigen Hundert liegt und am besten eine Primzahl ist. Die Nägel n sind fortlaufend nummeriert. Die Aufgabe besteht darin, für alle n von 1 bis p – 1 einen Faden von Nagel n zu Nagel 2n zu ziehen.
Ein Beitrag von Christoph Pöppe
Natürlich wird man das nicht der Reihe nach für n = 1, 2, 3, … machen, sondern in der Reihenfolge 1, 2, 4, 8, … Dann muss man nämlich nicht jedes Mal den Faden abschneiden und festknoten. Wer den Faden zieht, kommt ziemlich bald, nämlich wenn die erste Zweierpotenz den Wert p überschreitet, in die Verlegenheit, modulo p zu rechnen. Das wiederum wird durch die kreisförmige Anordnung der Nägel nahegelegt. Und wenn p nicht gerade eine Zweierpotenz plus 1 ist, dann findet der Faden erst dann zum Nagel 1 zurück, wenn er bereits alle anderen Nägel genau einmal besucht hat. Wieso?
Der Weg des Fadens wird periodisch Wenn der Faden einen nach n Schritten
Wenn der Faden einen nach n Schritten schon besuchten Nagel nach m Schritten nochmals trifft, dann ist 2m = 2n mod p, woraus 2m – n = 1 mod p folgt. Also wäre der Weg des Fadens bereits nach m–n Schritten periodisch. Erst wenn alle anderen Nägel bereits abgegrast sind, bleibt dem Faden nichts anderes übrig, als wieder bei Nagel 1 zu landen. Ja, diese Argumentation läuft auf einen Beweis des kleinen fermatschen Satzes hinaus. Mit einem echten Faden ist man selbst für mäßig große Werte von p eine gute Weile beschäftigt. Weniger geduldige Menschen setzen dafür den Computer ein. Es hilft der Übersicht, wenn man das Fadenstück von einem Nagel zum nächsten in Abhängigkeit von seiner Länge einfärbt.
Literatur-Tipp
Christoph Pöppe: „Das Einmaleins im Kreis.“ Spektrum der Wissenschaft 7/2022, S. 74–79,
Simon Plouffe: „The shape of bn mod p.“
So entstehen Kardioiden
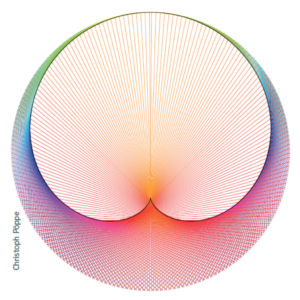
Was einem beim – echten oder virtuellen – vollendeten Fadenbild ins Auge springt, ist eine hübsche Kurve: die Kardioide, auch „Herzkurve“ genannt (s. Bild 1). Bemerkenswerterweise ist die Kurve selbst nicht Bestandteil des Bildes; vielmehr sind die einzelnen Fadenstücke Tangenten an die Kurve.
So entstehen Epizykloiden
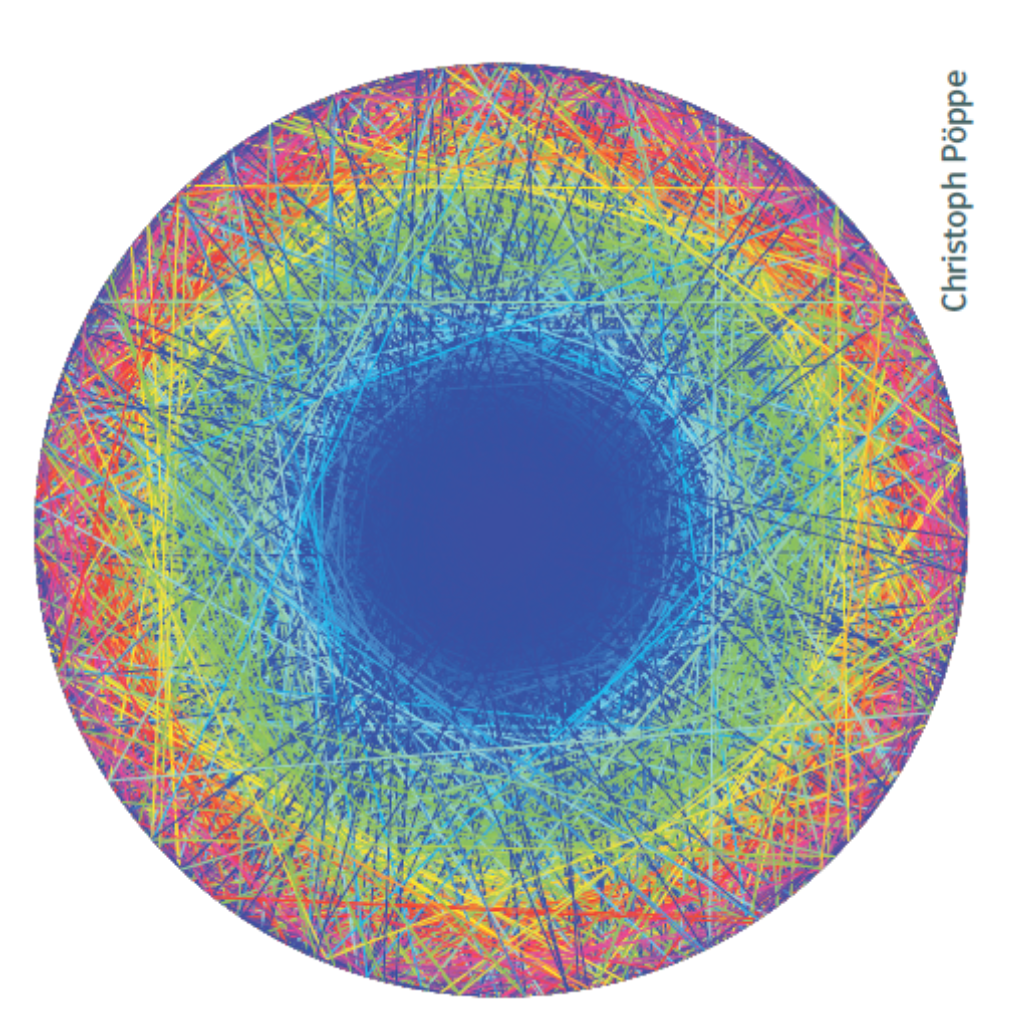
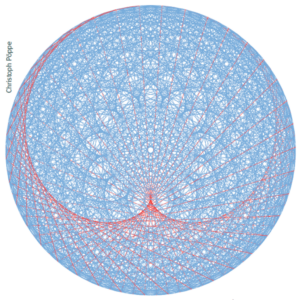
Eine Verallgemeinerung bietet sich an: Man ersetzt den Multiplikator 2 durch eine beliebige natürliche Zahl b. Bereits bei den ersten Versuchen stellt sich heraus: Aus der Kardioide mit der einen nach innen gerichteten Spitze werden Kurven mit b – 1 Spitzen. Es handelt sich um Epizykloiden; das sind die Kurven, die ein am Umfang eines Kreises befestigter Bleistift aufs Papier zeichnet, wenn dieser Kreis auf einem anderen Kreis abrollt. Mit wachsendem b wird der Innenkreis immer größer und der auf ihm abrollende Außenkreis entsprechend immer kleiner, sodass die immer zahlreicheren einwärts gerichteten Spitzen zu einer kaum noch sichtbaren Girlande am Rand des großen Kreises verkümmern. Stattdessen tauchen im Inneren des Kreises neue Strukturen auf, die auf den ersten Blick an gotische Spitzbögen erinnern (s. Bild 2 und Bild 3).


So entstehen konzentrische Kreise
Mit der Struktur von bn modulo p hat sich der französische Mathematiker Simon Plouffe intensiv befasst. Wenn b – 1 ein Teiler von p ist, es also eine natürliche Zahl k gibt, sodass p = k(b – 1) ist, dann entsteht ein Muster von konzentrischen Kreisen (s. Bild 4). Doch warum ist das so? Wir schreiben die Zahl n zur Basis k, genauer: als ku + v, wobei v zwischen 0 und k–1 liegt. Die Differenz bn – n = (b – 1)n schreibt sich dann folgendermaßen: (ku + v)(b – 1) = k(b – 1)u + v(b – 1) = pu + v(b – 1) Modulo p gerechnet, fällt der erste Term weg, also kommen für die Differenz bn – n überhaupt nur k verschiedene Werte vor, einer für jeden Wert von v. Die Differenz bn – n ihrerseits bestimmt die Länge des Strichs im Einheitskreis und diese wiederum dessen minimalen Abstand vom Kreismittelpunkt. Diese minimalen Abstände sind die Radien der Kreise, die so auffällig ins Auge springen.
So entstehen überlagerte Rollkurven
Setzen wir jetzt b eins höher, so ergibt sich ein deutlich erkennbares Spitzbogenmuster (s. Bild 5). Auch für diesen Fall hilft die Zerlegung von n zur Basis k. Wenn man nämlich jeden Strich entsprechend seinem v-Wert einfärbt, stellt sich heraus, dass das ganze Muster in k gegeneinander verdrehte Kardioiden zerfällt, eine für jeden Wert von v. Wenn man b weiter erhöht, wird aus der Kardioide eine zweispitzige Rollkurve, dann eine dreispitzige und so weiter. Wenn man also von allen möglichen Werten von n nur jeden k-ten verwendet, passt das Muster in das Schema mit den einfachen Rollkurven, das für kleine Werte von b funktioniert. Andere Muster entsprechen merkwürdigerweise einem b-Wert von zum Beispiel 2/3, was auf einen Kreis hinausläuft, der den festen Kreis umgibt und mit seiner Innenseite an ihm entlangrollt. Weitere Erklärungsmöglichkeiten harren noch ihrer Entdeckung. Simon Plouffe hat aus seiner reichhaltigen Bildersammlung ein paar Erfahrungsregeln hergeleitet, aber noch keine Begründung dafür. Es bleibt also noch viel auszuprobieren.
Fadenspiele und Kryptografie
Bemerkenswerterweise hat dieses Spiel mit merkwürdigen Mustern eine Beziehung zur modernen Kryptografie. Zu gegebenen Werten von b und p ist die Funktion f(n) = bn mod p relativ einfach auszurechnen, deren Umkehrung (der „diskrete Logarithmus“) dagegen sehr schwer: Es gibt praktisch keine bessere Möglichkeit, als alle Werte von n der Reihe nach durchzuprobieren. Eine leicht zu berechnende Funktion, deren Umkehrung in akzeptabler Zeit nicht zu finden ist, heißt „Falltürfunktion“; auf solchen Funktionen beruhen zahlreiche Verschlüsselungsverfahren. Dort geht es allerdings um p-Werte in der Größenordnung 21.000. Auch in diesem Fall gibt es für kleine b die bekannten Fadenmuster. Aber die Möglichkeit, dass es von diesen Ausnahmen abgesehen Strukturen im Fadenbild gäbe, die die Berechnung des diskreten Logarithmus vielleicht abkürzen könnten, kann man getrost ausschließen.
Zum Weiterlesen
Tatsächlich gibt es Künstler*innen, die sich die Mühe eines Fadenspiels machen, einer von ihnen ist John Eichinger:
Hier lassen sich Fadenspiele online erstellen:












