Je größer die Frequenz einer schwingenden Klaviersaite, umso höher ist der Ton, den der Mensch hört. Allerdings steigt die Tonhöhe nicht gleichmäßig mit der Frequenz an, sondern wird vom Gehör logarithmisch abgeflacht.
Ein Beitrag von Prof. Dr. Heinrich Hemme
Nach den Gesetzen der Mathematik ist die Summe der Logarithmen zweier Zahlen gleich dem Logarithmus ihres Produktes: log a + log b = log(ab). Die Erhöhung eines Tones um eine Oktave entspricht einer Verdopplung seiner Frequenz. Addiert man zu einem Ton 1, 2, 3, 4 oder allgemein n Oktaven, muss man darum seine Frequenz mit 21, 22, 23, 24 oder 2n multiplizieren. Jede Oktave der gleichstufig temperierten Tonleiter ist in zwölf Halbtöne gleichen Abstands unterteilt. Um von einem Halbton zum nächsten zu gelangen, muss man zu ihm eine Zwölftel Oktave addieren und darum seine Frequenz mit 21 ⁄ 12 = 12√2 ≈ 1,05946 multiplizieren
So lassen sich alle Frequenzen berechnen
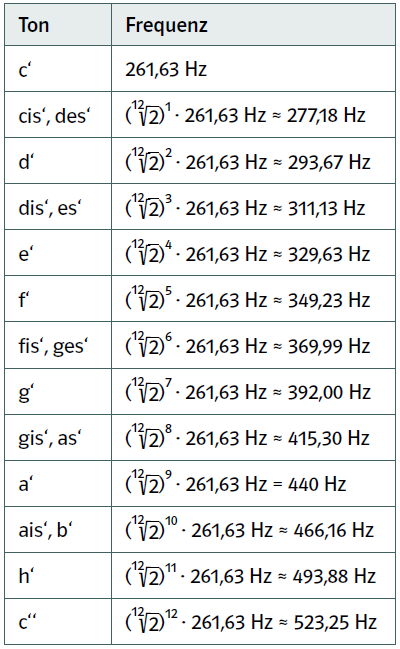
Die Frequenz des Kammertons aʻ ist auf 440 Hz normiert. Daraus ergeben sich die Frequenzen aller anderen Töne. Für cʻ bekommt man dadurch die Frequenz ½ 4√2 · 440 Hz ≈ 261,63 Hz und für die gesamte eingestrichene Oktave die Frequenzen der folgenden Tabelle.
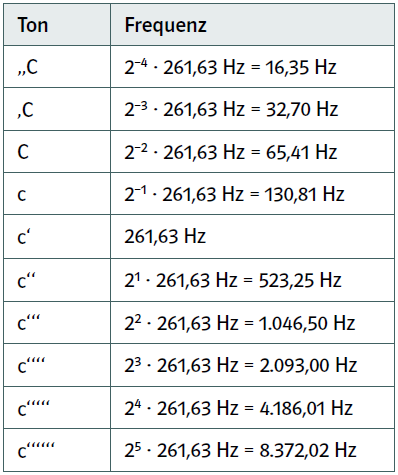
Die niedrigen und höheren Oktaven von der Subkontraoktave bis zur sechsgestrichenen Oktave beginnen mit den Tönen aus der folgenden Tabelle.
Im Prinzip gibt es noch beliebig viele Oktaven unterhalb der Subkontraoktave und oberhalb der sechsgestrichenen Oktave, aber ihre Töne sind für den Menschen unhörbar.
Wie die Frequenzen, so die Papierformate
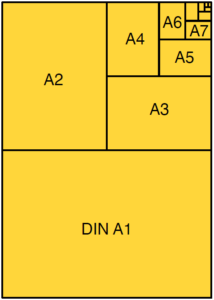
Wechseln wir kurz das Thema und gehen dazu vom Konzertsaal ins Büro. Die Papierformate sind seit 1922 in Deutschland normiert nach DIN 476 und von den meisten Ländern der Welt in ähnlicher Form übernommen worden. Sie wurden von dem Ingenieur und Mathematiker Walter Porstmann entwickelt. Das Grundmaß aller Papierformate ist ein rechteckiger Bogen von 1 Quadratmeter Größe, dessen Seitenlängen im Verhältnis 1 : √2 zueinander stehen. Sein Format wird als A0 bezeichnet. Halbiert man einen A0-Bogen parallel zu seinen kurzen Seiten, erhält man zwei A1-Bögen. Auch die Seiten des A1-Bogens stehen wieder im Verhältnis 1 : √2 zueinander. Dass das Seitenverhältnis genau 1 : √2 ist, hat einen guten Grund: Nur dann bleibt bei der Halbierung eines Bogens das Seitenverhältnis erhalten. Durch weitere Halbierungen erhält man die anderen A-Formate. Einen einzelnen A0-Bogen kann man also so zerschneiden, dass man je ein Blatt aller anderen Formate von A1 bis A∞ erhält.
Vom Zweidimensionalen zum Dreidimensionalen
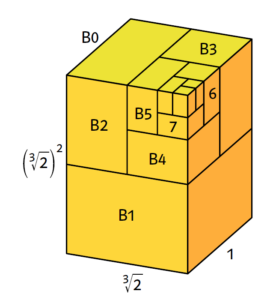
Was man im Zweidimensionalen machen kann, sollte man auch im Dreidimensionalen versuchen. Wir gehen darum vom genormten Rechteck zum genormten Quader. Das Grundmaß aller dreidimensionalen Formate ist ein B0-Quader von 1 Kubikmeter Volumen. Halbiert man ihn parallel zu seinen kleinsten Flächen, entstehen zwei B1-Quader, deren Kanten im selben Verhältnis zueinander stehen wie die Kanten des B0-Quaders. Durch fortgesetzte
Halbierung bekommt man die Quader von B2 bis B∞, die alle die gleichen Kantenlängenverhältnisse haben. Man kann leicht überprüfen, dass dies die Verhältnisse 1 : 3√2 : (3√2)2 sein müssen.
Von der Mathematik zurück zur Musik
Eduard Baumann aus Fribourg in der Schweiz ist noch einige Dimensionen weiter nach oben gestiegen. Das Vorstellungsvermögen
des Menschen versagt dort zwar, aber die Mathematik hat damit keinerlei Probleme. Baumann stellte fest, dass bei einem zwölfdimensionalen Hyperquader, der beim Halbieren seine Kantenverhältnisse bewahren soll, die Kanten im Verhältnis 1 : 12√2 : (12√2)2 : (12√2)3 : … : (12√2)11 stehen müssen. Der K0-Hyperquader hat ein Hypervolumen vom 1 m12. Damit war Baumann in der Musik gelandet. Nimmt man einmal an, dass 1 m gerade 11.502,76 Hz entspricht, dann sind die Kantenlängen des K0-Hyperquaders genau die Frequenzen 8.372,02 Hz, 8.869,84 Hz, …, 15.804,27 Hz der sechsgestrichenen Oktave. Halbiert man den Hyperquader, bekommt man zwei K1-Hyperquader. Ihre Kanten sind alle um einen Halbton kürzer und haben als Längen die Frequenzen der Halbtöne hʻʻʻʻʻ, cʻʻʻʻʻʻ, cisʻʻʻʻʻʻ, dʻʻʻʻʻʻ, …, aʻʻʻʻʻʻ und aisʻʻʻʻʻʻ. Auch jede weitere Halbierung der Hyperquader kürzt alle Kantenlängen um jeweils einen Halbton. Nach zwölf Halbierungen gelangt man zum Hyperquader K12, dessen Kantenlängen die Frequenzen der fünfgestrichenen Oktave sind. So geht dies immer weiter: Nach jeweils zwölf Halbierungen sind alle Kantenlängen eines Hyperquaders um eine Oktave kürzer geworden, bis man schließlich beim K108- Hyperquader und der Subkontraoktave angelangt ist. Nun könnte man ja erwarten, dass durch diesen geradezu ästhetischen Zusammenhang zwischen den DIN-A-Papierformaten und der Musik Noten auf DIN-A-Papier gedruckt würden. Das ist aber mitnichten so: Notenblätter haben bedauerlicherweise ganz andere Papierformate.

Prof. Dr. Heinrich Hemme
Prof. Dr. Heinrich Hemme ist Physiker und Unterhaltungsmathematiker. Er hat etwa 2.500 Artikel und rund 30 Bücher geschrieben, darunter Mathematische Kopfnüsse (Petersberg, 2022).












