von Heinrich Hemme
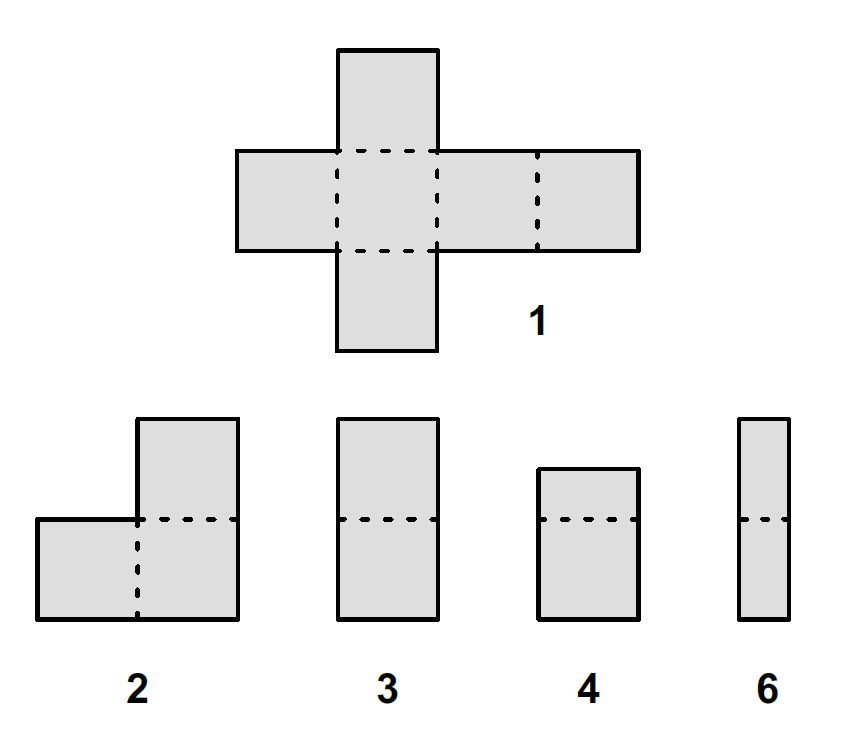
Der Amerikaner Martin Gardner (1914–2010) schrieb über 25 Jahre lang für das Wissenschaftsmagazin Scientific American die Kolumne „Mathematical Games“, in der er unterhaltsam über die Mathematik berichtete und mathematische Spielereien und Knobeleien vorstellte. Gardner wurde weltbekannt, Hunderttausende lasen begeistert seine Kolumne. Im Dezember 1990 stellte er den Leser*innen der Zeitschrift Cubism For Fun das folgende knifflige Problem: Ein Würfel lässt sich mit drei rechteckigen Aufklebern, die alle die Größe von zwei Würfelflächen haben, so bekleben, dass kein Stück seiner Oberfläche unbedeckt bleibt und außerdem die Aufkleber nirgendwo doppelt liegen. Es ist auch sehr leicht, mit zwei, drei, vier oder sechs deckungsgleichen Aufklebern eine Würfeloberfläche vollständig abzudecken, ohne dass die Aufkleber sich überlappen. Die Abbildung zeigt für jeden Fall ein Beispiel. Doch kann man auch mit jeder anderen Anzahl, also fünf, sieben, acht, neun, zehn, … von deckungsgleichen Aufklebern einen Würfel komplett, aber überlappungsfrei bekleben?
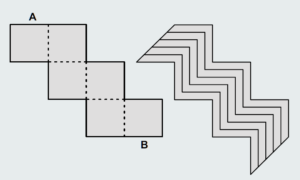
Eines der elf möglichen Würfelnetze hat ein treppenförmiges Aussehen. Faltet man es zu einem Würfel zusammen, stößt die Kante A an die Kante B. Deshalb kann man auch von dem linken oberen Quadrat eine Hälfte diagonal abschneiden und
an das untere rechte Quadrat wieder anhängen und behält trotzdem eine Figur, die sich zu einem Würfel falten lässt. Diese Figur kann man nun in eine beliebige Anzahl treppenförmiger deckungsgleicher Streifen zerschneiden. Mit diesen Streifen lässt sich ein Würfel entsprechender Größe vollständig und überlappungsfrei bekleben.