Wenn ein Hund nicht auf dem kürzesten (geraden), sondern auf dem zeitoptimalen (geknickten) Weg ins Wasser springt, um den Ball zu apportieren, löst er ein Minimierungsproblem. Das ist immerhin so kompliziert, dass es als Klausuraufgabe im zweiten Semester Analysis taugt. Und da kommt Timothy Pennings, Mathematikprofessor an einer kleinen Universität im ländlichen Michigan, und behauptet, sein Hund Elvis könne das auch!
Ein Beitrag von Dr. Christian Pöppe
Und dies kann Timothy Pennings immerhin durch ein korrekt durchgeführtes Experiment belegen. Er verschaffte seinem Hund Auslauf am Ufer des nahe gelegenen Michigansees, steckte mit dem Maßband eine Strecke am Ufer ab, warf, mitsamt dem Hund an der Wasserlinie stehend, einen Tennisball in den See und bestimmte sowohl dessen Position als auch den Punkt, an dem Elvis vom Laufen zum Schwimmen überging. Zusätzlich maß ein Helfer mit der Stoppuhr die Zeiten, die Elvis für beide Teilstrecken benötigte. Der hielt immerhin drei Stunden und 35 Messzyklen ohne Anzeichen von Ermüdung durch, und das bei einer Geschwindigkeit von durchschnittlich 6,4 Metern pro Sekunde an Land und 0,91 im Wasser. Das Ergebnis: Elvis findet die mithilfe der Analysis berechnete schnellste Route mit großer Genauigkeit. Dass er in der Tat die Zeit bis zum Erreichen des Balls optimiert und nicht etwa den eigenen Kraftaufwand, muss man aus seiner freudigen Erregung und seinem erwartungsvollen Hundeblick erschließen. Timothy Pennings zog mit öffentlichen Vorträgen zu diesem Thema durchs Land, die Herzen des Publikums flogen dem Hund – und vielleicht ein bisschen der Analysis – zu, und Elvis wurde berühmt. Im Gefolge von Pennings’ erster Veröffentlichung spekulierten Fachkollegen, ob der Hund die Ungleichung von Cauchy-Schwarz oder gar etwas Verzweigungstheorie und Variationsrechnung beherrsche, und die Nachricht von seinem Tod schaffte es sogar bis in die überregionale Presse.
Wie lassen sich Elvis’ „mathematische Fähigkeiten“ erklären?
Alles sehr nett; aber natürlich glaubt niemand im Ernst, Elvis würde in seinem Hundekopf die Laufzeit nach dem Absprungpunkt differenzieren, die Ableitung gleich null setzen und so weiter. Wie macht er es dann? Was physikalische Systeme so gern tun: irgendeine Energie minimieren, das tut Elvis nun gerade nicht – im Gegenteil. Photonen minimieren ihre Laufzeit von A nach B, auch wenn ihr Weg beim Übergang von Luft nach Glas einen Knick macht. Aber die machen ja auch Gebrauch von der Analysis, jedenfalls nach der Pfadintegraltheorie von Richard Feynman. Das Photon geht nicht nur den klassischen Weg, sondern sehr viele andere. Die zugehörigen Wahrscheinlichkeitswellen integrieren sich alle auf, und man beobachtet ein Photon da, wo konstruktive Interferenz stattfindet. Das ist da, wo das Integral über eine Menge fast gleicher Wellenfunktionen geht, das heißt wo die Ableitung der Laufzeit nach einem geeigneten Parameter gleich null ist: Minimum der Laufzeit.

Nein, Elvis versteht auch nichts von Wahrscheinlichkeitstheorie und Statistik. Aber es sieht fast so aus.

Elvis minimiert nicht seinen Kraftaufwand! Sonst
hätte er vielleicht einen kleineren Ast gewählt.
Also: Quantenmechanische Systeme können irgendwie Analysis. Aber für ein quantenmechanisches System ist Elvis viel zu groß. Vielleicht kann Elvis aus jeder Position einschätzen, welcher Weg ihn am schnellsten dem Ziel näher bringt, genauer, welche von zwei Geschwindigkeiten die größere ist: schwimmend direkt aufs Ziel zu oder die in Richtung Ziel weisende Komponente seiner Laufgeschwindigkeit an Land. Die letzte Größe nimmt ab, je näher er dem Ball kommt, bis auf null, wenn der Ball genau querab liegt. Irgendwann (Zwischenwertsatz) sind beide Größen gleich, und das ist der Absprungpunkt. Im Prinzip muss der Hund nur über die Fähigkeit verfügen, Geschwindigkeiten und deren Verhältnis einzuschätzen, was ihm ohne Weiteres zuzutrauen ist. Vor allem müsste er keinen Überblick über die Gesamtsituation haben, sondern käme mit lokalen Informationen aus. Die schöne Theorie wird durch die Realität widerlegt.
Auf dem Rückweg müsste nämlich Elvis, weil er mit lokaler Information – er ist im Wasser – den Vorteil des Landwegs nicht erfassen kann, den geraden, zeitaufwendigeren Weg wählen. Tut er aber nicht.
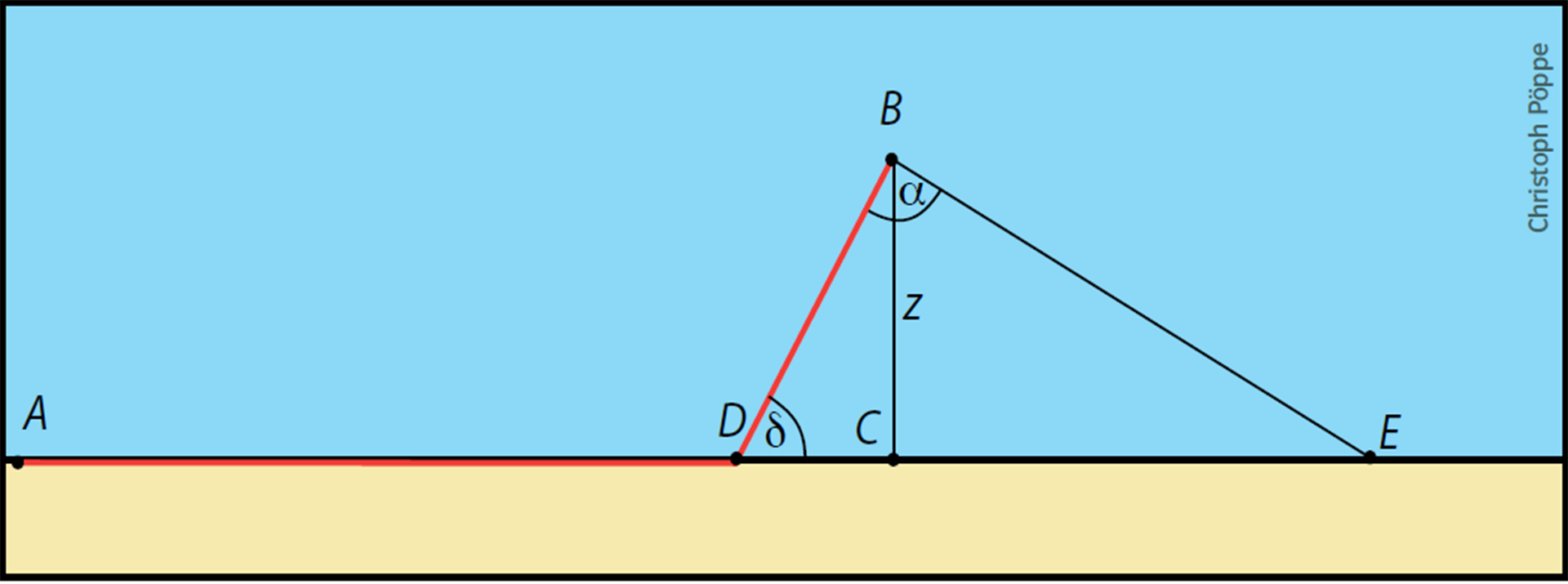
Dieses Diagramm zeigt den Laufweg A–D–B des Hundes ebenso wie die Laufzeit A–D–E. Der Maßstab ist so gewählt, dass der Hund an Land die Geschwindigkeit 1 hat.
Wie macht Elvis es nun wirklich?
Alda Carvalho und zwei ihrer Kollegen von der Universität Lissabon suchten und fanden eine Lösung ohne Analysis. Sie zeichneten den Weg des Hundes und die für jeden Teil dieses Wegs benötigte Zeit in dasselbe Diagramm. Oder, was auf dasselbe hinausläuft, sie dachten sich einen fiktiven Hund, der zeitgleich mit Elvis und mit derselben Geschwindigkeit losrennt, aber nicht ins Wasser abbiegt, sondern mit der Landgeschwindigkeit weiterläuft, bis Elvis am Ziel ist. In diesem Moment ist der „Schattenhund“ am Punkt E angelangt. Die Gesamtlaufzeit entspricht im gewählten Maßstab der Strecke AE. Deren Länge gilt es zu minimieren oder, was auf dasselbe hinausläuft, die Länge von CE. Die Portugiesen wenden nun den Sinussatz im Dreieck DEB an und kommen nach einigen Umformungen auf das Ergebnis

Dabei ist c = r/s das Verhältnis von Laufzu Schwimmgeschwindigkeit. An dieser Formel kann man die Lösung sofort ablesen. CE ist minimal, wenn sin α maximal ist; und das wiederum ist der Fall, wenn α ein rechter Winkel ist. Den Sinussatz kann Elvis zwar auch nicht – muss er aber auch nicht. Ein rechtwinkliges Dreieck wie DEB wird durch die Höhe CB in zwei Dreiecke zerlegt, die dem ursprünglichen Dreieck ähnlich sind. Also gilt
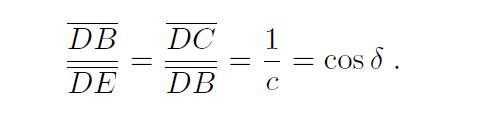
Literatur und Links
Bacinski, S. J. et al. (2015). Elvis Lives: Mathematical Surprises Inspired by Elvis, the Welsh Corgi. In: The College Mathematics Journal 46, Heft 2, S. 82–91.
Carvalho, A. et al. (2017). The Geometer Dog Who Did Not Know Calculus. In: The College Mathematics Journal 48, Heft 5, S. 339–345.
Elvis does calculus. – YouTube-Video
Pennings, T. J. (2003). Do Dogs Know Calculus? In: The College Mathematics Journal 34, Heft 3, S. 178–182.
Perruchet, P., Gallego, J. (2006). Do Dogs Know Related Rates Rather than Optimization? In: The College Mathematics Journal 37, Heft 1, S. 16–19.
Pöppe, C. (2021): Kann der Hund Analysis? In: Spektrum der Wissenschaft 7/2021, S. 86–89.
Zhou, L. (2017). Did Elvis Know Cauchy–Schwarz? In: The College Mathematics Journal 48, Heft 5, S. 335–338.
Damit ist klar, wie Elvis vorgehen muss: Er springt ins Wasser, wenn der Ball ihm, von seiner bisherigen Laufrichtung am Ufer entlang aus gesehen, unter dem Winkel 𝛿 erscheint. Dieser Winkel ist sozusagen eine persönliche Eigenschaft von ihm, denn cos 𝛿 = 1/c ist das Verhältnis von Schwimm- zu Laufgeschwindigkeit. Natürlich muss er diese Winkelfunktion nicht ausrechnen, sondern kann seinen optimalen Winkel 𝛿 durch Versuch und Irrtum erlernen. Wie machen es die Menschen? Wahrscheinlich ungefähr so wie die Hunde, jedenfalls ohne Analysis. Oder rechnen Sie erst das Minimum des Zeitaufwands aus, bevor Sie sich entscheiden, die Abkürzung über die Wiese anstelle des vorgesehenen Fußgängerwegs zu wählen? Oder wie schräg Sie eine Straße überqueren, in der es gerade keinen Autoverkehr gibt? Bei der letzten Frage wäre schon die mathematische Modellierung schwierig.

Dr. Christoph Pöppe
Jahrgang 1953, hat Mathematik und Physik studiert. Von 1989 bis 2018 war er (der einzige) Redakteur für Mathematik und verwandte Gebiete bei der Zeitschrift „Spektrum der Wissenschaft“.












