Das eigene Wohnquartier mathematisch erkunden

Die vertraute Wohnumgebung bietet mit ihren Gebäuden, Plätzen und Parks immer wieder Anlass, diese unter mathematischen Gesichtspunkten zu erkunden. Im vorliegenden Beitrag werden beispielhaft hierzu verschiedene Aufgaben vorgestellt.

Ein Beitrag von Christoph Maitzen

Wir Menschen benutzen tagtäglich die gleichen Wege zum Einkaufen, zur Schule oder zur Arbeit. Viele Fassaden oder Ansichten sind uns vertraut. Mathematische Themen wie Symmetrie, Winkel, Flächen, Volumen sowie Schätzen und Runden können Anlass sein, einen anderen – einen mathematischen Blick auf das uns bekannte Wohnquartier zu werfen.

Das Wohnquartier mit einem mathematischen Blick betrachten

Eine Möglichkeit ist es, Schüler*innengruppen mit einem offenen Arbeitsauftrag loszuschicken. Für das Thema Symmetrie könnte der Arbeitsauftrag lauten: „Geht in Dreiergruppen in die nähere Umgebung der Schule und fotografiert mit dem Handy Gegenstände, die Symmetrien zeigen. Ihr habt dafür 30 Minuten Zeit.“ Die Schüler*innengruppen kehren mit einer Vielzahl an Bildern zurück, die sie nun sichten sollen, um zwei bis drei besonders gelungene Bilder auszuwählen und der Klasse anschließend zu präsentieren.

Eine andere Möglichkeit ist es, Schüle*rinnengruppen zu ausgewählten Objekten in der näheren Schulumgebung zu schicken. Der Arbeitsauftrag könnte lauten: „Die Gruppe A geht in die XY-Straße Nr. Z., in der sich ein Fachwerkhaus befindet.

a) Notiere, welche geometrischen Flächen an der Fassade zu sehen sind.
b) Beschreibe und skizziere, welche Symmetrien und welche Symmetrieachsen an der Fassade zu erkennen sind.“

Die Gruppe könnte aufschreiben, dass sie an der Fassade Rechtecke, Dreiecke, verschiedene Halbkreise, Trapeze, Rauten und weitere zusammengesetzte Flächen sowie Flächen sieht, die durch Viertelkreise oder gekrümmte Linien begrenzt werden. Zu den Symmetrien und Symmetrieachsen könnten sie formulieren:

„Achsensymmetrisch sind die Fenster mit den Streben und die verschiedenen in weiß verputzten Formen, d. h. Rechteck, Halbkreise, Trapeze und die zusammengesetzten Flächen zwischen den dunklen Holzbalken. Der Giebel ist als Ganzes achsensymmetrisch gebaut.“ Für die meisten Schüler*innen wird es sicher einfacher sein, die Formen zu skizzieren und die Symmetrieachsen einzuzeichnen.

Größen abschätzen und überschlagen

Hin und wieder sind Gegenstände zu entdecken, die zu groß oder zu klein geraten scheinen, wie hier im Beispiel ein übergroßes Hufeisen. Hier ergeben sich Anknüpfungspunkte für fantasievolle Fragestellungen.

Zu einem Hufeisen an einer Hauswand könnte die Aufgabe lauten: „Die geflieste Fläche hat eine Breite von etwa 6,6 Meter. Schätze durch eine Rechnung ab, wie groß in etwa ‚das Pferd‘ zu dem Hufeisen an der Wand sein müsste.“ Zur Lösung der Aufgabe ist die Breite des Hufeisens an der Wand abzuschätzen, wobei die Fliesenanzahl abgezählt werden kann:

Für ein reales Pferd sind die Hufeisenbreite (ca. 15 Zentimeter) und die Pferdegröße (Widerrist – erhöhter Übergang vom Hals zum Rücken: ca. 1,7 Meter) zu recherchieren.

Mit diesen Werten ergibt sich:

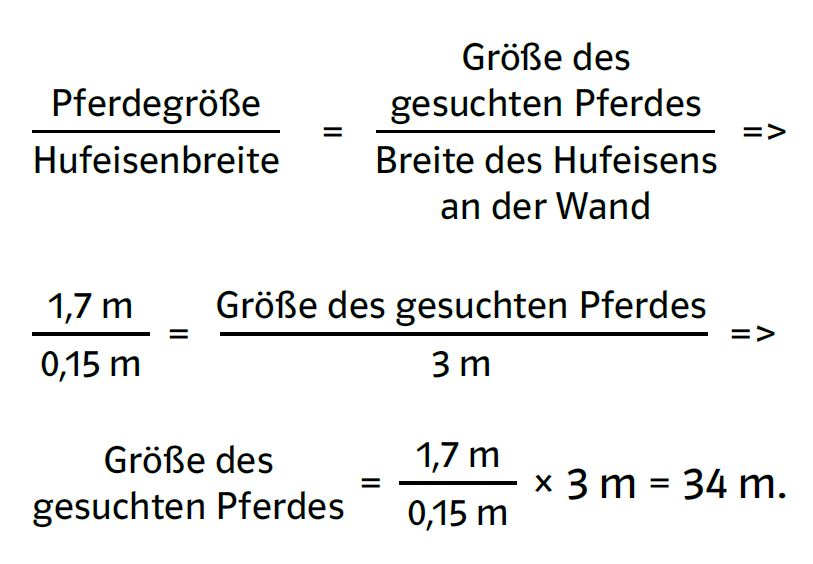
Typische Größen schätzen können

Im Alltag kommt es immer wieder vor, dass die Raumhöhe oder eine Wandlänge abzuschätzen ist. Hier bieten die Maße einer Tür oder eines Fensters Anhaltspunkte für eine erste Abschätzung. Im Außenbereich des Wohnumfelds können Länge und Breite von Mauer- oder Pflastersteinen sowie Gehwegplatten Schätzlängen für die Überschlagsrechnung anbieten. Für den abgebildeten Pflanzkübel könnte die Aufgabe lauten: „Zur Verschönerung von Fußgängerzonen werden vor den Geschäften Pflanzkübel mit einer quadratischen Grundfläche aufgestellt. Die Pflasterung der Fußgängerzone besteht aus Pflastersteinen mit einer Breite von ca. zehn Zentimetern. Schätze mithilfe einer Rechnung das Innenvolumen des Pflanzkübels ab.“

Ausgehend von der angegebenen Pflastersteinbreite ergibt sich sofort für die untere Kante des Pflanzkübels mit vier Pflastersteinen eine Breite von etwa 40 Zentimetern. Der Pflanzkübel hat die Form eines Pyramidenstumpfes. Um die Rechnung einfach zu gestalten, kann das Volumen durch einen Quader mit quadratischer Grundfläche modelliert werden. Die mittlere Breite des Pflanzkübels kann aus der oberen und unteren Kantenlänge gewonnen werden. Das Längenverhältnis im Bild von oberer Kantenlänge zu unterer Kantenlänge beträgt etwa 1,5. Damit ist die obere Kante 1,5 × 40 Zentimeter, also 60 Zentimeter lang. Die mittlere Breite des Pflanzkübels beträgt somit

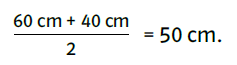
Auch Gegenstände auf einem Spielplatz wie dieser Durchgang in einer Holzwand (siehe Abbildung) eignen sich für interessante Schätzaufgaben: „Auf einem Kinderspielplatz befindet sich die auf dem Foto abgebildete Holzwand (Höhe 186 Zentimeter, Breite 150 Zentimeter). Der Durchgang ist 122 Zentimeter hoch und an der breitesten Stelle (grün gestrichenes Holz) 72 Zentimeter breit.

a) Berechne, wie groß die Holzfläche ohne Durchgang wäre (Angabe im m²).
b) Schätze durch eine Rechnung ab, wie groß die Fläche des Durchgangs etwa ist.“

Der erste Aufgabenteil stellt eine Annäherung an den Sachverhalt dar und soll die Umwandlung der Längen- bzw. Flächenmaße von Zentimeter in Meter bzw. Quadratzentimeter in Quadratmeter wiederholen. Der Lösungsweg könnte so aussehen:

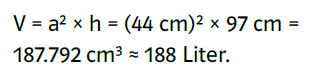
Für den zweiten Aufgabenteil gibt es grundsätzlich zwei Lösungsmöglichkeiten. Zum einen das Breitenverhältnis von der unteren Durchgangsbreite zur Holzwandbreite aus dem Foto durch Messen zu ermitteln, zum anderen die untere Durchgangsbreite optisch grob orientiert an der
Holzwandbreite abzuschätzen. Die erste Möglichkeit führt zur folgenden Rechnung: Das Breitenverhältnis von der unteren Durchgangsbreite zur Holzwandbreite aus dem Foto beträgt 5 zu 13. Damit ergibt sich für die untere Durchgangsbreite

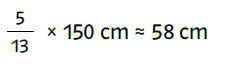
und damit weiter für die Durchgangsfläche

Die zweite Möglichkeit führt zu folgender Überlegung: Die breiteste Stelle des Durchgangs ist 72 Zentimeter breit, dies ist fast die Hälfte der Gesamtbreite von 150 Zentimetern. Die untere Durchgangsbreite ist aber deutlich schmaler als die breiteste Stelle des Durchgangs. Also vielleicht ein Drittel der Gesamtbreite oder etwas mehr, d. h. 55 Zentimeter. Damit ergibt sich eine Durchgangsfläche von

Die Fläche des Durchgangs liegt dann etwa bei 7.000 Quadratzentimetern oder 0,7 Quadratmetern.

Was bringt es?

Mit den dargestellten Beispielen möchte ich Lehrer*innen anregen, mit ihrer Lerngruppe das eine oder andere Mal eine Erkundung in die nähere Umgebung ihrer Schule oder im Rahmen eines Ausfluges zu unternehmen. Anlässlich des aktuellen Unterrichtsthemas (Winkel, Symmetrie, mathematische Formen oder Körper, Steigung, …) können Schüler*innen in Kleingruppen auf eine mathematische Entdeckungsreise gehen. Nebenbei erfahren die Lernenden, dass es in ihrer Lebensumwelt und in ihrem Wohnquartier viele und unterschiedliche Bezüge zur Mathematik gibt.

Über den Autor

Christoph Maitzen

ist Diplom-Physiker und arbeitet als Gymnasiallehrer für die Fächer Mathematik und Physik an der Ziehenschule in Frankfurt/Main. Er ist Mitherausgeber der Fachzeitschrift „Mathematik 5–10“ (Friedrich Verlag) und aktiv im Verein Mathematik-Unterrichts-Einheiten-Datei (MUED.de). Seit 2008 veröffentlicht er als Autor Fachartikel, Fach- und Schulbücher.

Beitrag teilen:

Ähnliche Beiträge

Über Visualisierungen Problemlöseprozesse im MINT-Unterricht unterstützen

19. Mai, 2023

Der Unterricht der naturwissenschaftlichen Fächer verläuft häufig problemorientiert. Das bedeutet, es werden Problemlöseprozesse durchlaufen, in denen die Lernenden zunächst mit einer realen, authentischen oder konstruierten Problemsituation konfrontiert werden, aus der sich ein oder mehrere Fragestellungen ergeben, die für die Lernenden nicht auf Anhieb lösbar sind. Was sie aber leisten können, ist, auf der Basis ihres Vor- oder Alltagswissens Ideen, Vermutungen oder gar Hypothesen zur Fragestellung zu formulieren, diese dann durch Auswertung empirischer Daten zu prüfen und über die erhaltenen Ergebnisse die Fragestellung(en) zu beantworten.

Weiter lesen

Mit einem Escape Game die Ursachen und Folgen des Klimawandels verstehen

15. April, 2023

Der Klimawandel beschreibt die langfristigen Veränderungen von Faktoren wie der Temperatur, des Niederschlags und der Meeresströmungen. Er schreitet bedrohlich schnell voran, trifft vor allem besonders vulnerable Gruppen und betrifft uns alle. Längst ist von einer Klimakrise die Rede, die die Gesundheit, Sicherheit und Ernährung, ja die gesamte Existenz der Menschheit bedroht. Wir alle bekommen den Klimawandel im wahrsten Sinne des Wortes zu spüren. Laut Angaben des Weltklimarates IPCC (Intergovernmental Panel on Climate Change) sind 3,3 bis 3,6 Milliarden Menschen auf der Welt „hochgradig gefährdet“.

Weiter lesen

Wie uns Entchen zu den Müllstrudeln der Welt führen

14. April, 2023

Eine verlorene Schiffsladung ist nicht nur ein Ärgernis für die Reederei, in den meisten Fällen hat solch ein Ereignis zudem negative Folgen für die Umwelt. Im Januar 1992 gelangten durch einen Sturm etwa 28.800 Kunststofftiere ins Meer. Unter dem Namen „Friendly Floatees“ wurden sie weltbekannt und halfen der Wissenschaft, die windgetriebenen Oberflächenströmungen besser zu verstehen.

Weiter lesen

LE-Klett-Mint-Kampagne-Header-4-1920x1080px

Gesponserte Inhalte

Wichtige Kompetenzen für den weiteren Bildungsweg fördern

5. April, 2023

In der Grundschule sollen die Schülerinnen und Schüler nicht nur Wissen erwerben, sondern vielmehr eine Reihe wichtiger Kernkompetenzen, die sie für ihren weiteren Bildungsweg und ihr folgendes Alltagsleben benötigen. Mit dem Lernkonzept SPIKE TM Essential von LEGO® Education gelingt es Lehrkräften leicht, spielerisch-entdeckendes Lernen in ihren Klassenzimmern zu fördern und den Kindern damit alle relevanten Fähigkeiten schnell und nachhaltig zu vermitteln.

Weiter lesen

Experimentieren fürs Klima – mit AdUmint zur klimafreundlichen Routenplanung

16. März, 2023

In den letzten Jahren scheint der anthropogene Klimawandel unsere Gesellschaft zu spalten. Der notwendige wissenschaftliche Diskurs geht zwischen Straßenblockaden und Demonstrationen in einem Gemenge von Meinungen und politischer Stimmungs-mache unter. Das Verständnis naturwissenschaftlicher Erkenntnisgewinnung kann nicht nur dazu beitragen, Ursachen und Auswirkungen des Klimawandels nachzuvollziehen, sondern bildet auch die Grundlage für eine aktive und wissenschaftlich fundierte Beteiligung am Klimaschutz.

Weiter lesen

LE-Klett-Mint-Kampagne-Header-3-1920x1080px

Gesponserte Inhalte

Forschendes Lernen mit Alltagsbezug – ein handlungsorientierter Ansatz

8. März, 2023

Grundschülerinnen und -schüler begreifen Dinge schneller, wenn sie Erfahrungen und Erlebnisse aus ihrem eigenen Alltag mit dem neuen Lernstoff verbinden können. Dann macht das Lernen mehr Spaß und ergibt für die Kinder einen alltagsbezogenen Sinn. Mit den bekannten LEGO® Steinen aus dem Lernkonzept SPIKETM Essential von LEGO Education können sie die ihnen bekannte Welt in realitätsnahen Modellen nachbilden und die zugehörigen Aufgaben mit Alltagsbezug lösen.

Weiter lesen

Gesponserte Inhalte

Teach Economy: Kostenloses Material für den digitalen Wirtschaftsunterricht

17. Februar, 2023

Ob fachlich geprüfte Unterrichtseinheiten oder dazu passende digitale Ergänzungen – das umfangreiche und kostenlose Angebot www.teacheconomy.de bietet spannende, didaktisch aufbereitete Materialien für den Wirtschaftsunterricht. Auch dieses Jahr wird das Teach Economy Team wieder mit einem Stand auf der didacta in Stuttgart vor Ort sein. Schauen Sie mal vorbei!

Weiter lesen

LE-Klett-Mint-Kampagne-Header-2-1920x1080px

Gesponserte Inhalte

Spaß am Programmieren entwickeln

13. Februar, 2023

Mit dem handlungsorientierten Lernkonzept SPIKE TM Essential von LEGO® Education können Sie Grundschulkindern elementare Aspekte der informatischen Bildung vermitteln, die für ein Verständnis der digitalen Welt immer wichtiger wird. In spannenden Unterrichtseinheiten, die auf die Lehrpläne abgestimmt sind, lernen die Kinder spielerisch die Grundlagen der Programmierung kennen und erwerben wichtige übergreifende, interdisziplinäre Fähigkeiten. Probieren Sie es auf der didacta bei Klett MINT selbst aus!

Weiter lesen

Gesponserte Inhalte

Spielend leicht digitalen Grundschulunterricht gestalten und in wenigen Minuten Programmieren lernen

23. Januar, 2023

Wer keinerlei Erfahrung mit digitalem Unterricht hat, der möchte das Thema oft gar nicht aufgreifen. Aber mit dem handlungsorientierten Lernkonzept SPIKE TM Essential von LEGO® Education gelingt es spielend leicht, Grundschulkindern der Klassen 1 bis 4 die Grundprinzipien des Programmierens beizubringen.

Weiter lesen

Mit Wärmebildkameras Lebensvorgängen auf der Spur

23. Januar, 2023

Mithilfe von Thermografie- oder Wärmebildkameras lässt sich die für unsere optische Wahrnehmung nicht erfassbare Infrarotstrahlung detektieren und sichtbar machen. Die von verschiedenen Gegenständen oder Lebewesen emittierte Wärmestrahlung wird durch die Programmierung der Kamera so umgerechnet, dass sogenannte Falschfarbenwärmebilder entstehen. Unterrichtliche Erfahrungen zeigen, dass Lernende diese Farbcodierung zumeist intuitiv verstehen.

Weiter lesen

Citizen Science – echte Forschungsprojekte in der Schule

5. Januar, 2023

Pinguine in der Antarktis zählen, Galaxietypen identifizieren oder Tiere der Serengeti bestimmen – Citizen Science bietet vielfältige Möglichkeiten zum Mitforschen für Schüler*innen.

Weiter lesen

Gesponserte Inhalte

Weltraumtechnologie im Unterricht Erdbeobachtung aus dem All

1. Dezember, 2022

Das Schulmaterial der Deutschen Raumfahrtagentur im DLR und Klett MINT erklärt anschaulich, wie Erdbeobachtung funktioniert und welchen Nutzen der Blick von oben für uns auf der Erde hat.

Weiter lesen