Wie kann man die Ebene lückenlos mit lauter gleichen Steinen bedecken, ohne periodisch zu werden? Neben den berühmten Penrose-Parketten gibt es eine große Vielfalt von Pflasterungen.
Ein Beitrag von Dr. Christian Pöppe
Hier geht es um lückenlose Füllungen der Ebene („Parkettierungen“), die aus lauter Exemplaren ein und derselben „Kachel“ bestehen – zuweilen ist es auch interessant, zwei verschiedene Sorten Kacheln zuzulassen. Und es sollen nicht die periodischen Muster sein, die man in jedem Badezimmer findet, und auch nicht die berühmten, zwingend nichtperiodischen Penrose-Parkette. Vielmehr sollen die hier beschriebenen Parkette von einem Zentrum aus in alle Richtungen „ausstrahlen“ – was immer das im Einzelfall heißen mag. Bemerkenswerterweise gibt es dazu keine abgeschlossene Theorie. Die „Bibel der Parkettierung“ von Grünbaum und Shephard (1987) bringt nur ein paar unvollständige Bemerkungen dazu, und reichlich 30 Jahre danach sind wir zwar um zahlreiche Beispiele reicher, aber die Situation bleibt unübersichtlich. Es gibt also noch jede Menge zu entdecken.
Torten und Ringe
Wenn Sie – zum Beispiel – 24 gleichschenklige Dreiecke mit einem Scheitelwinkel von 15 Grad so zusammenlegen, dass sich alle Spitzen in einem Punkt treffen, ergibt sich eine etwas eckige Torte. Die ist erweiterbar, und zwar mit denselben Dreiecken! Legen Sie um die Torte einen Ring aus abwechselnd einwärts und auswärts gerichteten Tortenstücken, um diese noch einen Ring und so weiter. Fertig ist das Radialparkett (siehe Bild 1). Zu allem Überfluss kann man die ganze unendliche Supertorte durch einen einzigen geraden Schnitt zweiteilen, ohne dabei ein Tortenstück anzutasten, und dann die beiden Hälften um eine lange Dreiecksseite gegeneinander verschieben. Dabei entsteht ein Spiralparkett:
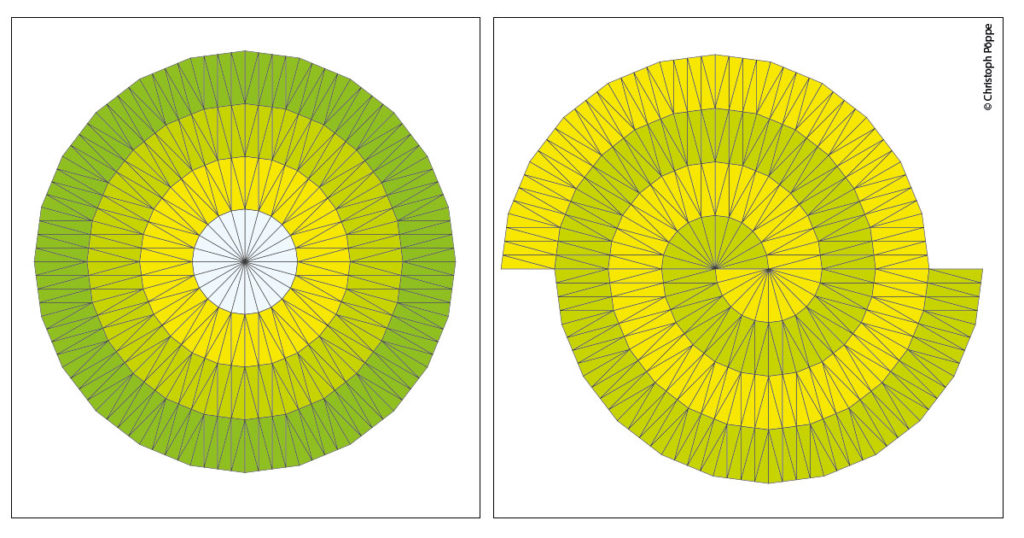
Zwei Schlangen treffen sich im Zentrum und winden sich umeinander bis ins Unendliche (siehe Bild 2). Wer um mehr als eine lange Dreiecksseite verschiebt, erhält eine entsprechend größere Anzahl an Schlangen. Das ist das elementarste Beispiel eines Radialbeziehungsweise Spiralparketts. Wie bei Parketten üblich, darf man die Seiten der Parkettsteine etwas deformieren, solange man das bei allen Seiten, die irgendwo im Parkett aneinander zu liegen kommen, in gleicher Weise tut. So darf man jede Seite eines Tortenstücks durch eine Kurve ersetzen, die dieselben Endpunkte hat und punktsymmetrisch zum Mittelpunkt der bisherigen Seite ist.
Mondsicheln und Matterhörner
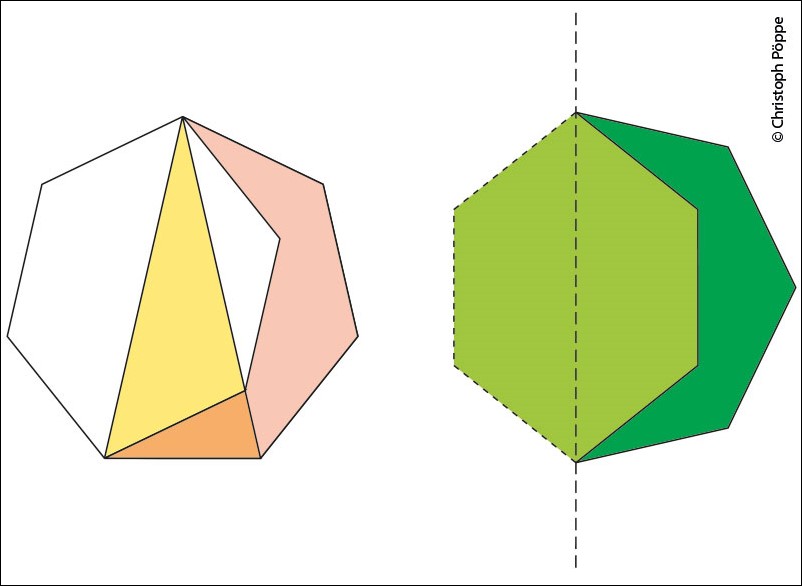
Damit ein Parkett nicht in die Periodizität gezwungen wird, muss man die Ursteine auf mehrere verschiedene Arten aneinanderlegen können – je mehr, desto besser. Von einem regelmäßigen (2n+1)-Eck spiegele man n Seiten nach innen (siehe Bild 3).
Die so entstehenden „Mondsicheln“ lassen sich parallel oder mehr oder weniger gegeneinander verdreht zusammenlegen. Das gibt dem Fliesenleger erhebliche Freiheiten (siehe Bild 4).

Für n-Ecke mit n = 6k stellt man fest, dass k Seiten des n-Ecks gerade zwei Ecken eines geeignet einbeschriebenen Sechsecks verbinden und daher auch jede dieser Ecken mit dem Mittelpunkt. Für n = 12 ergibt sich das, was der Schweizer Mathematikdidaktiker Hans Walser das „Matterhorn“ genannt hat. 12 Matterhörner ergeben wieder eine Torte (siehe Bild 5). An die kann man weitere Matterhörner nicht nur ringförmig anlegen, sondern auch „quer“, was weitere Möglichkeiten eröffnet. Für n = 24 ergibt sich das „Versatile“, mit dem der Brite Brian Wichmann eindrucksvolle Parkette legt (siehe Bild 6). Allerdings sind diese Bausteine nicht mehr spiegelsymmetrisch, mit dem Effekt, dass man in der Regel sowohl den Baustein als auch sein Spiegelbild als Pflastersteine einsetzen muss.
Oder man zerschneidet ein regelmäßiges n-Eck in Standard-Tortenstücke und deformiert deren lange Seiten zu Streckenzügen, die eine Folge von Seiten des n-Ecks bilden. Das funktioniert genau dann, wenn n ein Vielfaches von 6 ist. Warum? Beim regelmäßigen Sechseck ist die Verbindungsstrecke von Ecke zu Mittelpunkt genauso lang wie die Seite.
An die kann man weitere Matterhörner nicht nur ringförmig anlegen, sondern auch „quer“, was weitere Möglichkeiten eröffnet. Für n = 24 ergibt sich das „Versatile“, mit dem der Brite Brian Wichmann eindrucksvolle Parkette legt (siehe Bild 6). Allerdings sind diese Bausteine nicht mehr spiegelsymmetrisch, mit dem Effekt, dass man in der Regel sowohl den Baustein als auch sein Spiegelbild als Pflastersteine einsetzen muss.

Rautentorten
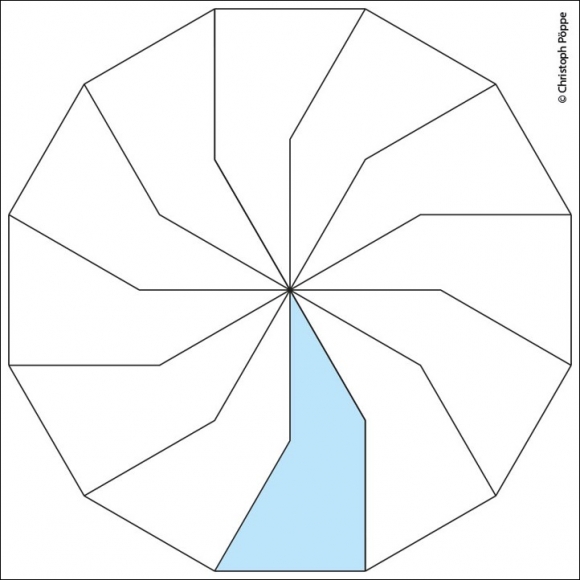
Ein weiteres, sehr ergiebiges Konstruktionsprinzip für Pflastersteine ergibt sich so: Man setze n gleiche Rauten mit einer spitzen Ecke in den Mittelpunkt, zum Beispiel indem man obige Tortenstücke an ihrer kurzen Seite spiegelt und dann Bild und Spiegelbild zusammenfasst. In die Lücken zwischen den Rauten setze man weitere Rauten, in die neu entstehenden Lücken wieder Rauten, und so weiter.Mit jeder Runde werden die Rauten breiter, bis das Anlegen ein „natürliches“ Ende in einer großen, n-eckigen Torte findet.
Zum selben Endergebnis kommt man, indem man ein regelmäßiges n-Eck n-mal mit dem Winkel 360°/n um eine seiner Ecken dreht. Eine geeignet gewählte Teilmenge der Rauten aus dem so entstehenden Muster ergibt einen vielseitig einsetzbaren Pflasterstein (siehe Bild 7). Durch die Konstruktion finden sich am Rand eines solchen Steins Streckenzüge, die aufeinanderfolgenden Seiten eines regelmäßigen n-Ecks entsprechen – was sich wie bei den Mondsicheln und den verallgemeinerten Matterhörnern als vorteilhaft erweist. Gelegentlich muss man auch hier zwei spiegelbildlich gleiche Steine aus dem Muster ausschneiden. Wenn man bereit ist, auch halbe Rauten zu verwenden, lässt sich eine überraschende Vielfalt von Pflastersteinen als Ausschnitt aus einem Rautenmuster interpretieren.
Literatur und Links
Branko Grünbaum, C. G. Shephard (1987)
Tilings and Patterns. New York:
Freeman.
Brian Wichmann. Spiral patterns.
www.tilingsearch.org/tree/t22.htm
Christoph Pöppe. Kunstvolle Spiralparkette.
Spektrum der Wissenschaft
1/2021, S. 82–86.
Die hier gezeigten Bilder sind nur ein kleiner Ausschnitt aus einer unübersehbaren Fülle von Radial- und Spiralparketten. Von einer umfassenden Theorie ist die Wissenschaft noch weit entfernt. Man hat bereits die größte Mühe, die Schlangen oder Spiralen, die man im günstigen Fall auf den ersten Blick sieht, mathematisch sauber zu definieren. Einstweilen dürfte es ein dankbares Projekt sein, neue Radial- und Spiralparkette zu ersinnen. Möglichkeiten dafür gibt es reichlich: Die meisten Steine sind so vielseitig verwendbar, dass man selbst dann noch verschiedene Fortsetzungsoptionen hat, wenn ein zentraler Bereich bereits festliegt.
Download
Linktipps Radial- und Spiralparkette | MINT Zirkel 2-2021
Über den Autor

Dr. Christian Pöppe
Jahrgang 1953, hat Mathematik und Physik studiert. Von 1989 bis 2018 war er (der einzige) Redakteur für Mathematik und verwandte Gebiete bei der Zeitschrift „Spektrum der Wissenschaft“.












