Was haben Quadratzahlen mit Farben zu tun?

Die moderne Physik des Lichts und der Atome begann nicht mit Albert Einstein und nicht mit Max Planck, sondern mit dem Schreib- und Rechenlehrer Johann Jakob Balmer.

Rund 150 Jahre nachdem Isaac Newton das Sonnenlicht in die Farben des Regenbogens zerlegt hatte, entdeckte Joseph von Fraunhofer im Spektrum des Sonnenlichts feine schwarze Linien, die den stetigen Übergang zwischen den Farbtönen unterbrechen. Fraunhofer wusste für sie keine Erklärung. Beim irdischen Spektrum eines glühenden Metallklotzes findet man sie nicht. Sie deuten auf etwas in der Sonne Verborgenes hin.

Wellenzahl der Lichtwelle

Mitte des 19. Jahrhunderts schließlich schlug Anders Jonas Ångström vor, verdünnte Gase leuchten zu lassen und deren Spektren zu betrachten. Je verdünnter die Gase waren, umso deutlicher hoben sich spezielle Farben ab. Ångström selbst vermaß beim Wasserstoff mit großer Präzision, in welchen Farben dieses Gas leuchtet. Die Vermessung der Farben erfolgte, indem Ångström angab, wie viele Wellenberge einer Lichtwelle auf einen Zentimeter passen. Man nennt dies die Wellenzahl. Es zeigte sich, dass Wasserstoff rot mit 15.233 als Wellenzahl sowie türkis mit 20.564, blau mit 23.032, indigo mit 24.373 und violett mit 25.181 als Wellenzahlen strahlt. Warum aber leuchtet es genau in den Farben dieser Wellenzahlen? Es lag nahe, dass es mit der Bauweise des Wasserstoffatoms zu tun hat. Aber mechanische Modelle, die seine Hülle als schwingungsfähige Membran nachbildeten, versagten. Bis 1885 blieb es rätselhaft, wie diese Wellenzahlen entstehen.

Lösung ohne physikalische Modellbildung

Johann Jakob Balmer, ein 60-jähriger Lehrer einer Basler Mädchenschule, löste das Rätsel. Er sah von physikalischen Modellen ab, er dividierte bloß die vier nachfolgenden Wellenzahlen 20.564, 23.032, 24.373 und 25.181 durch die erstgenannte 15.233 des roten Licht

20.564 : 15.233 = 1,34996…
23.032 : 15.233 = 1,51198…
24.373 : 15.233 = 1,60000…
25.181 : 15.233 = 1,65305…

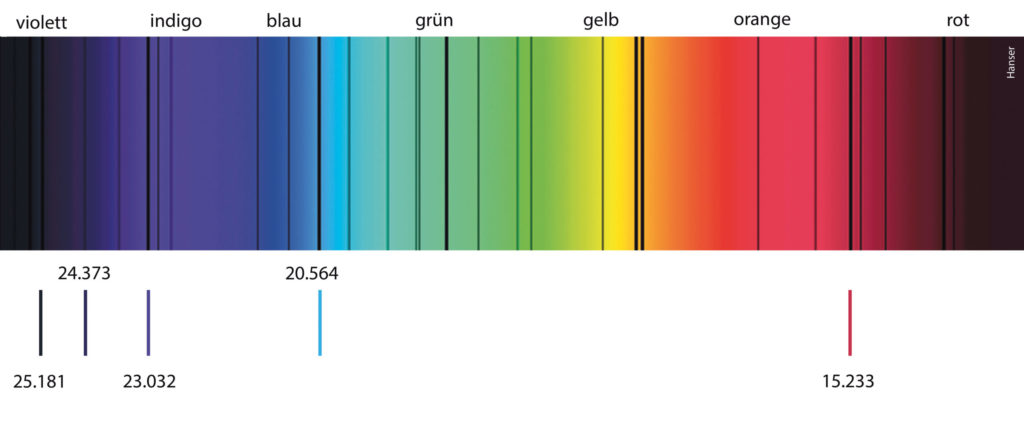
Einige der Fraunhoferschen Linien entsprechen den von Wasserstoff erzeugten Spektrallinien.

Die dritte Division lieferte das höchst auffällige Ergebnis 1,60000… Balmer, dem die Zahlenmystik nicht fremd war, glaubte, dass die Dezimalzahl 1,6, die sich aus der Division 16 : 10, gekürzt aus 8 : 5 ergibt, den „echten“ Wert darstellt, der sich bei einer völlig präzisen Messung ergäbe. Bei den beiden ersten Divisionen glaubte er auch, diesen „echten“ Wert erraten zu können, weil Rundungen der Ergebnisse dazu führen. Bei der ersten Division ist es die Dezimalzahl 1,35, die sich aus der Division 135 : 100, gekürzt aus 27 : 20 ergibt. Und bei der zweiten Division ist es die Dezimalzahl 1,512, die sich aus der Division 1.512 : 1.000, gekürzt aus 189 : 125 ergibt. Balmer sah die Nenner 20, 125 und 5 dieser gekürzten Divisionen und war wie elektrisiert: Es ist 20 = 5 × 4, und 4 ist eine Quadratzahl. Es ist 125 = 5 × 25, und 25 ist eine Quadratzahl. Es ist 5 = 5 × 1, und auch 1 ist eine Quadratzahl. Ein wenig schöner wäre es, so dachte Balmer, wenn der erste Nenner 80 = 5 × 16, der zweite Nenner wie gehabt 125 = 5 × 25 und der dritte Nenner 180 = 5 × 36 lauten würden. Dies lässt sich leicht verwirklichen, weil 27 : 20 das Gleiche wie 108 : 80 und weil 8 : 5 das Gleiche wie 288 : 180 ergibt. Und bei den Nennern 5 × 16, 5 × 25 und 5 × 36 sah Balmer die Quadratzahlen 16 = 4 × 4, 25 = 5 × 5 und 36 = 6 × 6 in aufsteigender Reihenfolge. Die nächste Quadratzahl ist 49 = 7 × 7. Balmer vermutete, dass sie bei der letzten Division dann im Nenner aufscheinen werde, wenn man vom gemessenen zum „echten“ Wert übergeht. Das überprüfte er. Er multiplizierte die vierte Wellenzahl 25.181 mit 49, was den Wert 1.233.869 ergibt, und dividierte diesen durch die Wellenzahl 15.233 des roten Lichts: 1.233.869 : 15.233 = 80,99973… Dass dies praktisch exakt mit 81 übereinstimmt, kann – davon war Balmer überzeugt – kein Zufall sein. Auch der „echte“ Wert der vierten Division ist entlarvt: Er lautet 81 : 49 oder, mit 5 erweitert, 405 : 245. Somit erriet Balmer die „echten“ Verhältnisse der vier nachfolgenden Wellenzahlen zu der des roten Lichts, nämlich 108 : 80 – 189 : 125 – 288 : 180 – 405 : 245 mit den Nennern 80 = 5 × 16 = 5 × 4 × 4 – 125 = 5 × 25 = 5 × 5 × 5 – 180 = 5 × 36 = 5 × 6 × 6 – 245 = 5 × 49 = 5 × 7 × 7.

Fundamentalzahl des Wasserstoffs

Jetzt stand Balmer vor der Aufgabe, die Wellenzahl 15.233 des roten Lichts, auf das er alle anderen Wellenzahlen bezog, selbst auf eine tragfähige Basis zu stellen. Auch diese Aufgabe löste er spitzfindig: Ihn störte bei seinen Nennern der Faktor 5, der ja keine Quadratzahl ist. Und er wunderte sich, dass man bei der dritten Division die Quadratzahl 36 erst künstlich durch Erweiterung einführen musste. Wie wäre es, so fragte er sich, wenn man die Divisionen nicht durch die Wellenzahl 15.233 des roten Lichts, sondern durch jene Zahl vollzieht, die sich aus der Multiplikation von 15.233 mit 36 und nachträglicher Division durch 5 ergibt? Die so erhaltene Dezimalzahl 109.677,6 nannte Balmer die „Fundamentalzahl des Wasserstoffs“. Heute wird sie nach Johannes Rydberg, einem schwedischen Physiker, benannt.

Geheimnis der Wellenzahlen des Wasserstoffs

Was die Division der Wellenzahl des roten Lichts durch die Fundamentalzahl des Wasserstoffs ergibt, ist klar: Es ist jenes Verhältnis 5 : 36, mit der Balmer zur Fundamentalzahl des Wasserstoffs gelangte. Die Division der Wellenzahl des türkisen Lichts durch die Fundamentalzahl des Wasserstoffs läuft auf die Rechnung hinaus, dass man 108 : 80 mit 5 zu multiplizieren und durch 36 zu dividieren hat. Hier ist es schön, dass 108 : 36 = 3 und 80 : 5 = 16 sind. Somit kam Balmer auf das Verhältnis 3 : 16. Er erweiterte es zu 12 : 64, weil der Nenner 64 die nächste gerade Quadratzahl nach 36 ist. In ähnlicher Weise ging Balmer bei den restlichen drei Verhältnissen vor. Bei der Division der Wellenzahl des blauen Lichts durch die Fundamentalzahl des Wasserstoffs kam er auf das Verhältnis 21 : 100. Dies ist in seinen Augen ein treffliches Ergebnis, denn 100 ist, auf 64 folgend, die nächste gerade Quadratzahl. Bei Indigo kam er auf das Verhältnis 2 : 9, das er mit 16 erweitert und zu 32 : 144 umformt. Hier ist der Nenner 144 die auf 100 folgende nächste gerade Quadratzahl. Schließlich kam er bei der Division der Wellenzahl des violetten Lichts durch die Fundamentalzahl des Wasserstoffs auf das Verhältnis 45 : 196. Auch das ist in seinen Augen ein passendes Ergebnis, denn 196 ist, auf 144 folgend, wiederum die nächste gerade Quadratzahl. Und als Balmer seine Ergebnisse 5 : 36 = 5 : (9 × 4); 12 : 64 = 12 : (16 × 4); 21 : 100 = 21 : (25 × 4); 32 : 144 = 32 : (36 × 4); 45 : 196 = 45 : (49 × 4) betrachtete, war er vollends überzeugt, das Geheimnis der Wellenzahlen des strahlenden Wasserstoffs in seiner ganzen Tiefe gelüftet zu haben: Die Nenner dieser Verhältnisse sind die Produkte der Quadratzahl 4 mit den nach ihr folgenden Quadratzahlen 9, 16, 25, 36 und 49. Und die Zähler dieser Verhältnisse sind die Differenzen der Quadratzahl 4 von den Quadratzahlen 9, 16, 25, 36 und 49. Die Wellenzahlen des strahlenden Wasserstoffs erhält man, so lautet Balmers Gesetz, wenn man die Fundamentalzahl 109.677,6 des Wasserstoffs mit den Verhältnissen (9 − 4) : (9 × 4); (16 − 4) : (16 × 4); (25 − 4) : (25 × 4); (36 − 4) : (36 × 4); (49 − 4) : (49 × 4) multipliziert. Es sind die Quadratzahlen 4, 9, 16, 25, 36, 49, die für die Farben strahlender Gase sorgen.

Prof. Dr. Rudolf Taschner setzte sich als Professor an der Technischen Universität Wien und als Initiator und Betreiber des Projekts math.space erfolgreich dafür ein, dass die Mathematik möglichst vielen Menschen zugänglich wird.

Lese-Tipp

Rudolf Taschner. Die Farben der Quadratzahlen. Kleine Anleitung zum mathematischen Staunen
München: Hanser 2019, 268 Seiten, 22 Euro

Beitrag teilen:

Ähnliche Beiträge

CO2-Schleuder Biokraftstoff – eine Studie sorgt für Gesprächsstoff

14. März, 2023

Biokraftstoff gilt als umwelt- und klimafreundliche Alternative zu fossilen Treibstoffen. Denn weil er aus Pflanzen erzeugt wird, gibt er bei seiner Verbrennung kaum mehr Kohlendioxid ab, als die Pflanzen zuvor bei ihrem Wachstum aufgenommen haben – so jedenfalls die Theorie. Doch gibt es bei der Sache vielleicht einen Haken?

Weiter lesen

Die Erde im Visier außerirdischer Zivilisationen

7. März, 2023

Was wissen extraterrestrische Intelligenzen von uns, falls es sie gibt? Vielleicht mehr, als uns lieb ist, denn über 2.000 Sterne in der näheren Umgebung haben eine privilegierte Position, von der aus sich die Erde studieren lässt. Zu 75 davon sind bereits irdische Radiosendungen gelangt.

Weiter lesen

Matheschmerz-Prophylaxe: Holen Sie einen Roboter an Ihre Schule!

13. Februar, 2023

Youtuber Daniel Jung beschäftigt sich mit „Matheschmerz“, weil Mathe bei vielen Versagensängste hervorruft. Die Psychologin Bettina Hannover berichtet, dass Jugendliche sich vorstellen, dass jemand mit Physik als Lieblingsfach keine Freund*innen hat und unattraktiv aussieht. Und „Digital-kunde“ ist in Deutschland immer noch nicht als Pflichtfach etabliert, obwohl die Diskussion um Web 5.0 schon begonnen hat. MINT-Lehrkräfte haben es wirklich nicht einfach, obwohl diese Kenntnisse für immer mehr Berufe sehr gefragt oder sogar eine Voraussetzung sind.

Weiter lesen

Vanadium-Redox-Flow-Batterien als neue Lösung zur Energiespeicherung

10. Februar, 2023

Weltweit steigende Temperaturen, vermehrt auftretende Dürren und Extremwetterereignisse: Eine der größten Herausforderungen der heutigen Zeit ist der Klimawandel, der hauptsächlich durch die menschengemachten Emissionen von klimaschädlichen Gasen verursacht wird. Ein großer Teil dieser Emissionen wird durch das Verbrennen von fossilen Energieträgern freigesetzt. Erneuerbare Energien wie Wind-, Wasser- oder Solarenergie leisten ihren Beitrag zur Energiewende. Allerdings treten insbesondere Solar- und Windenergien oft mit tages- und jahreszeitlichen Schwankungen auf.

Weiter lesen

Nomen est omen – von Walfischen und Reptilien

29. Januar, 2023

Mithilfe von Thermografie- oder Wärmebildkameras lässt sich die für unsere optische Wahrnehmung nicht erfassbare Infrarotstrahlung detektieren und sichtbar machen. Die von verschiedenen Gegenständen oder Lebewesen emittierte Wärmestrahlung wird durch die Programmierung der Kamera so umgerechnet, dass sogenannte Falschfarbenwärmebilder entstehen. Unterrichtliche Erfahrungen zeigen, dass Lernende diese Farbcodierung zumeist intuitiv verstehen.

Weiter lesen

Jagd nach einem neuen „Planet Nine”

13. Januar, 2023

Jenseits des Neptuns wurden Tausende Himmelskörper gefunden, wo bis vor 30 Jahren nur der neunte Planet Pluto beheimatet schien. Der wiederum ist längst kein Planet mehr – schauen wir uns die Revolutionen am Rande des Sonnensystems einmal genauer an.

Weiter lesen

Jelly Falls – gelatinöses Zooplankton als Kohlenstoffsenke

16. Dezember, 2022

Wenn man von der Kohlenstoffsenke hört, denkt man zunächst an Wälder, Moore oder gar an die Gletscher, doch ein wichtiger Kontributor ist der Ozean, im Speziellen die Tiefsee. Die Tiefsee kann man sich wie eine Wüste vorstellen. Es ist ein Ort der Extreme, mit hoher Salinität, niedrigen Temperaturen und enormem Druck. Doch der eigentliche limitierende Faktor für organisches Leben in der Tiefsee ist die Nahrungsverfügbarkeit, die ab 1.000 Meter Tiefe nahezu verschwindend gering ist. Dementsprechend sind Tiefseeorganismen auf jede Nahrungsquelle angewiesen. Und genau hier kommen Quallen ins Spiel.

Weiter lesen

Warum Karl der Große mein Ururur…großvater ist

9. Dezember, 2022

Nach der Bibel waren die ersten beiden Menschen Adam und Eva, und sie sollen vor etwa 6.000 Jahren gelebt haben. Doch kann das sein?

Weiter lesen

Bleiben oder gehen? Wie uns der Klimawandel in Bewegung setzt

18. November, 2022

Jeder dritte Mensch ist aufgrund des Klimawandels und der damit einhergehenden Bedrohung der Lebensgrundlage ausgesprochen verwundbar – das zeigt der Weltklimarat IPCC in seinem neuesten Sachstandsbericht zum Thema „Klimawandel 2022: Folgen, Anpassung und Verwundbarkeit“. Was das für unsere Zukunft bedeutet und warum das oberste Ziel nicht unbedingt lautet, Migration zu verhindern, klärt dieser Beitrag.

Weiter lesen

Warum der Straßenverkehr immer komplexer wird

26. Oktober, 2022

Über viele Jahrzehnte war der Verkehr, insbesondere der auf der Straße, ein Thema, das zwar ständig auf der Tagesordnung stand, aber nicht als „kritisch“ angesehen wurde. Die individuelle Mobilität und die dazugehörigen Angebote wurden als selbstverständlich eingestuft. Natürlich gab es auch mal Einschränkungen, man denke nur an die beiden Ölkrisen in den 1970er-Jahren, die zu deutlichen Rezessionen führten. Die Bevölkerung trug die Maßnahmen mit und es trat nach einiger Zeit wieder Entspannung ein. Doch wie sieht das heute aus?

Weiter lesen

Der menschliche Faktor oder wie berufliches Miteinander gelingen kann

28. Juni, 2022

Es ist unumstritten: Beruflicher Erfolg hängt von einer guten Ausbildung ab. In den letzten Jahrzehnten hat allerdings auch der Wert von sozialen Fähigkeiten wie Kooperationsbereitschaft erheblich zugenommen. Fähigkeiten wie diese lassen das berufliche Miteinander besser gelingen. Und dafür sind typische menschliche Verhaltensmuster verantwortlich.

Weiter lesen

Kollision der Giganten

8. Juni, 2022

Die Zukunft der Milchstraße wird turbulent – erst stößt sie mit der Andromeda-Galaxie zusammen, später auch mit der Triangulum-Galaxie. Hier ein Vorausblick auf den Crash der Sterneninseln.

Weiter lesen