Man stelle sich vor, man zieht gerade um und auch das Sofa soll mit. Es wäre ja auch zu schön, wenn alles glattlaufen würde. Und so passiert’s: Das Sofa passt im Flur nicht um die Ecke. Aber wie kann das ein ungelöstes Problem der Mathematik sein?
Für ein gegebenes Sofa kann man leicht nachrechnen, ob man hängen bleibt oder nicht. Die offene Frage ist, wie groß die Grundfläche eines solchen Sofas maximal sein kann, damit es um die Ecke eines Flurs der Breite 1 passt. Während eine exakte Lösung nicht bekannt ist, kann man einige Aussagen bezüglich der gesuchten maximalen Fläche treffen.
Als Mathematiker trifft man zunächst Annahmen. Erst mal wollen wir nur starre Gegenstände zulassen. Um weniger von Verhältnissen der Größen von Flur und Sofa reden zu müssen, legen wir die Breite des Flurs auf 1 fest; und zwar „vor“ und „hinter“ der Ecke, die genau rechtwinklig sein soll. Für die Grundfläche eines Sofas schreiben wir A.
Geschickt rotieren
Um sich an das Problem heranzuwagen, kann man jetzt mal ausprobieren, was funktioniert. Ein Würfel mit Seitenlängen 1, d. h. A = 1 ⨯ 1 = 1, passt um die Ecke, wenn man ihn von der einen Seite so weit schiebt wie möglich und dann von der anderen Seite der Ecke weiterzieht. Wir sehen an diesem Beispiel: Die maximale Grundfläche beträgt auf jeden Fall mindestens 1 (A ≥ 1). Ist es vielleicht möglich, einen größeren Gegenstand zu nehmen? Nein, denn man kann noch einen größeren Gegenstand konstruieren, den man um die Ecke schieben (rotieren) kann. Das Rotieren geht so: Nimmt man einen Halbkreis mit Radius 1 – mit der flachen Seite zur inneren Seite der Ecke – und schiebt ihn bis zur gegenüberliegenden Wand, dann kann man ihn an der unteren Ecke um die Ecke ziehen. So finden wir eine Fläche der Größe A = π/2 ≈ 1,571, was schon mal deutlich größer als 1 ist.
Telefonhörer statt Sofa
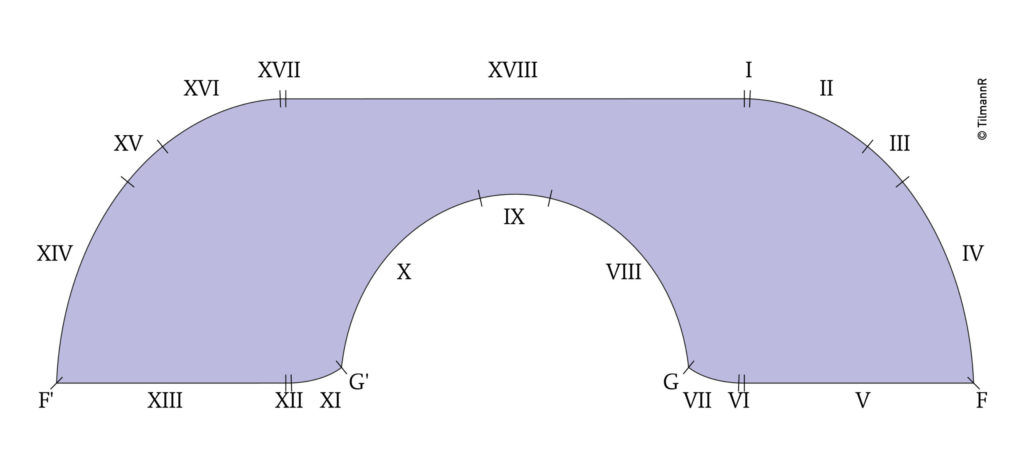
Aber man kann noch weiter kommen: John Hammersley, Mathematiker in Oxford, hat ein Objekt in der Form eines (alten) Telefonhörers konstruiert, dessen Fläche π/2 + 2/π ≈ 2,207 beträgt. Der Trick besteht darin, an der Innenseite eine passende Aussparung einzubauen, die sich an der spitzen Ecke entlang bewegen kann. Der „Telefonhörer“ besteht einfach aus zwei Viertelkreisen an den Seiten und einem Rechteck in der Mitte, aus dem innen ein Halbkreis „herausgefräst“ wurde. Diese einfache Konstruktion hat der amerikanische Mathematiker Joseph Gerver verfeinert, indem er eine optisch ähnliche Form aus 18 Kurvensektionen zusammengesetzt hat. Die vielen Kurvensektionen sind nötig, um den Platz auf der anderen Seite optimal auszunutzen. Damit kommt er auf eine leicht größere Fläche von A ≈ 2,219. Hammersley hat sich auch bemüht, eine möglichst niedrige Obergrenze für die maximale Fläche zu finden. Als solche obere Schranke hat er 2 √2 ≈ 2,828 identifiziert. Man beachte den überraschend schönen (d. h. kürzen) Zahlausdruck. Vor Kurzem, im Jahr 2017, haben jedoch zwei Mathematiker eine niedrigere obere Schranke von 2,37 ermittelt. Wo zwischen 2,219 und 2,37 liegt nun das wahre Maximum? Man weiß es nicht. Vielleicht kann man mit Kreativität und eigenen Ideen die Konstruktion weiter verbessern. Oder eventuell etwas über ein erweitertes Problem herausfinden; zum Beispiel für den Fall, dass am Ende des Flurs eine weitere Ecke in die andere Richtung folgt – dann muss der Telefonhörer auch auf der anderen Seite ausgefräst werden und ähnelt einer 8.
Das Problem ist jedenfalls ein gutes Beispiel für anschauliche und leicht zu verstehende Probleme der Mathematik, die man mit komplexen Methoden behandeln kann, um dann am Ende klare Aussagen über die Realität treffen zu können. In der Mathematik gibt es viele solche Probleme, die ungelöst sind. Wer sich in die Probleme selbst hineindenkt und einen Ansatz findet, den andere bisher übersehen haben, kann zur Forschung eigene Resultate beitragen.
Tim M. Baumgartner, Deutsches Jungforschernetzwerk – juFORUM e. V.












