Wie bekommt man, was man will? Oder wie erhöht man zumindest seine Chancen? Spieltheorie liefert ebenso hilfreiches wie spannendes Wissen zu diesen Fragen.
Eine Dinner-Party. Die Gäste sitzen gesellig beieinander, als die Teenager-Tochter des Hauses die Treppe herunterkommt und „Tschüss“ ruft. Der Vater und Gastherr der Party fragt: „Wo gehst du hin?“ – „Weg“, ist die knappe Antwort. Nach ein paar langen Sekunden antwortet der Vater: „Okay, tschüss.“ Diese Episode während der Dinner-Party, amüsant beschrieben von einem der Autoren des Lehrbuchs „Games of Strategy“ (aus dem einige der folgenden Beispiele stammen), ist ein klassisches Beispiel für ein Strategiespiel. Die Tochter möchte abends ausgehen und denkt sich eine entsprechende Strategie aus, um die Zustimmung der Eltern zu bekommen. In diesem Fall riskiert die Tochter ganz bewusst, einen Streit vor Gästen anzuzetteln, bei dem sowohl sie als auch ihr Vater eine schmachvolle Niederlage erleiden könnten. Aber die Tochter kennt ihren Vater gut genug, um zu vermuten, dass er diesen Streit würde vermeiden wollen. Sie sollte recht behalten, denn ihr Vater gibt relativ schnell den Widerstand auf. Langjährige Erfahrung, gute Kenntnisse über den Gegenspieler oder auch einfach Intuition sind viel gebrauchte Wegweiser in Strategiespielen. Da aber viele Menschen – Tennisspieler, Geschäftsleute, Politiker und nicht zuletzt Kriegsparteien – sich Strategien zurechtlegen, um in Wettbewerben mit hohen Einsätzen ihre Erfolgschancen zu erhöhen, ist es nicht überraschend, dass Wissenschaftler eine formalisierte Theorie entwickelt haben. Diejenige Theorie, die sich mit Strategie befasst, heißt kurioserweise „Spieltheorie“; obwohl sie am wichtigsten ist, wenn es bitterernst ist. Im Kalten Krieg benutzte die USA zum Beispiel eine Version des Feiglingsspiels (Game of Chicken). In der ursprünglichen Version dieses Spiels rasen zwei Autofahrer aufeinander zu. Wer als Erster ausweicht, hat verloren. Mathematisch lässt sich dieses Spiel folgendermaßen darstellen:

Jeder Fahrer hat die Wahl zwischen Draufhalten und Ausweichen. Wenn beide Fahrer draufhalten, ist der Verlust für beide am größten (-2). Wenn ein Fahrer ausweicht, verliert er (-1), während der andere Fahrer ungeschoren davonkommt und das Spiel gewinnt (2). Sollten beide Fahrer ausweichen, kommen sie beide mit heiler Haut davon, aber keiner gewinnt (0). In der Kubakrise drohten die USA zum Äußersten zu gehen – dem Atomkrieg – , sollten die UdSSR nicht ihre Atomwaffen aus Kuba abziehen. Eingeweihte haben später erzählt, dass die Welt nie so nah am Atomkrieg war wie damals. Aber zum Glück funktionierte die amerikanische Abschreckungspolitik: die UdSSR lenkte ein. Lehrkräfte hingegen spielen jedes Mal ein Strategiespiel, wenn ein Schüler verspätet Hausaufgaben abgeben möchte. Die folgende Tabelle gibt die Punkte für einen fiktiven Schüler und Lehrer wieder.
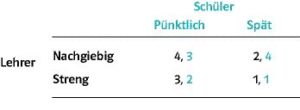
Lehrende und Lernende haben eine Vorstellung davon, wie sich der jeweils andere verhalten wird, und basieren ihr Verhalten auf diese Erwartung. Die beste Situation für diesen Lehrer ist es, wenn der Schüler die Hausaufgaben pünktlich erledigt, ohne dass er streng werden muss (oben links). Wenn er erwartet, dass der Schüler so oder so die Hausaufgaben verklüngelt, ist seine beste Strategie auch Nachgiebigkeit (oben rechts). Falls der Schüler zu spät abgibt, ist der Autoritätsverlust des Lehrers nämlich schlimmer, wenn er vorher Strenge angedroht hat (unten rechts). Folglich ist nachgiebig sein die dominante, d. h. bei beiden Verhaltensweisen des Schülers beste Strategie für den Lehrer. Dieser Argumentation folgend, hat der Schüler guten Grund, auf die Milde des Lehrers zu hoffen; immerhin ist Nachgiebigkeit die dominante Strategie dieses Lehrers. Der Schüler kann sich also Zeit lassen mit seinen Hausaufgaben (oben rechts). Aller Voraussicht nach endet dieses Spiel also damit, dass der Schüler seine Hausaufgaben zu spät abgibt und der Lehrer Milde walten lässt (oben rechts). Das ist das sogenannte Nash-Gleichgewicht dieses Spieles. Keiner der beiden Spieler kann seine Situation dadurch verbessern, dass er im Alleingang seine Strategie ändert.
Das Gleichgewicht verschiebt sich
Das Verzwackte an diesen Strategiespielen ist, dass dieses Nash-Gleichgewicht (sofern es eines gibt) oft suboptimal ist oder schlimmstenfalls eine Katastrophe bedeutet. Zusammen betrachtet ständen Schüler und Lehrer am besten da, wenn der Schüler trotz fehlender Strenge des Lehrers pünktlich die Hausaufgaben abgibt (oben links). Wie lässt sich diese Situation erreichen beziehungsweise das Nash-Gleichgewicht dahingehend verschieben? Unter der Voraussetzung, dass das Spiel mehrmals gespielt wird – der Schüler also öfter als ein Mal eine Hausaufgabe beim gleichen Lehrer abgeben muss –, hat ein Spieler zwei Strategien zur Auswahl: Entweder er kann sich auf eine Strategie festlegen, die er standardmäßig spielt, oder aber er kann vorab ankündigen, wie er auf jeden Zug des anderen Spielers reagieren wird. Wenn der Lehrer sich für die erste Strategie entscheidet und sich vorab festlegen möchte, kann er somit Strenge als Standardstrategie festlegen und Nachgiebigkeit als Option ausschließen. Es ist wichtig, dass der Lehrer diese Entscheidung laut und deutlich ankündigt, sodass der Schüler weiß, was ihn erwartet, und seine Strategie entsprechend wählt. Darüber hinaus muss der Schachzug des Lehrers sichtbar und unumkehrbar sein. Zum Beispiel könnte sich der Lehrer auf die Schulordnung berufen, nach der er nur streng und keinesfalls nachgiebig sein kann. Imgrunde entspricht die alternative Strategie (eine Vorankündigung, wie der Lehrer auf das Verhalten des Schülers reagieren will) entweder einer Drohung oder einem Versprechen. Wenn der Lehrer etwa eine gesonderte Note für Hausaufgaben einführt, die in die Gesamtnote einfließt, werden die Folgen größer, weil der Schüler im Voraus weiß, wie der Lehrer auf jede seiner Entscheidungen – die Hausaufgaben rechtzeitig oder zu spät abgeben – reagieren wird. Schlägt man an einem x-beliebigen Tag die Zeitung auf, handelt mit ziemlicher Sicherheit mindestens ein Artikel von Strategiespielen. Zum Beispiel spielt der russische Präsident Putin ein Feiglingsspiel mit dem NATO-Verbund, in dem er das NATO-Mitglied Türkei mit winzigen Luftraumverletzungen provoziert. Sollte die Türkei einen Krieg anzetteln, um sich zu verteidigen, wären die NATO-Partner durch den Eintritt des Bündnisfalls gezwungen, sich an dem Krieg mit Russland zu beteiligen, was einer Eskalation gleichkäme.
Die US-Vorwahl als Beispiel
Donald Trumps Konkurrenten im Kampf um die Ernennung zum republikanischen Präsidentschaftskandidaten, Ted Cruz und John Kasich, sind ebenfalls in ein klassisches Feiglingsspiel verwickelt: Solange beide im Rennen sind, kosten sie einander Stimmen. Wenn einer der beiden aufgäbe, würde er die Chancen des anderen erhöhen, gegen Trump zu gewinnen. Geben aber beide nicht auf, trüge Trump mit größerer Wahrscheinlichkeit den Sieg davon. Für beide Kandidaten wäre es das weitaus schlechteste Ergebnis. Kenntnisse von Spieltheorie helfen also jedem Zeitungsleser, die Hintergründe und Folgen des Gelesenen besser zu verstehen. Die obigen Beispiele zeigen, dass es sich außerdem für jedermann, einschließlich Schülern und Lehrern, lohnt, das eigene Handeln mit Abstand zu betrachten und überlegt zu agieren. Nicht zuletzt fördert strategisches Denken auch die Empathie, da man gezwungen ist, sich in die anderen Spieler hineinzuversetzen.
Dieser Beitrag gibt die persönliche Auffassung der Autorin
Dr. Frauke Hoss wieder












