In der Epidemiologie ist Mathematik ein unverzichtbares Instrument zur Analyse und Prognose der Ausbreitung von ansteckenden Krankheiten, aus der sich konkrete Handlungsempfehlungen für den Alltag ableiten. Die gegenwärtige Pandemie ermöglicht daher eine Vermittlung mathematischer Inhalte mit hohem Aktualitätsbezug, wie z. B. Berechnungen zur Überlastung des Gesundheitssystems sowie der Wahrscheinlichkeit von Superspreading-Ereignissen durch größere Menschenansammlungen.
Schon die elementare Dreisatzrechnung hilft bei der Bewertung der Sinnhaftigkeit bestimmter Ansätze, wie z. B. die am Anfang der CoV-2-Pandemie diskutierte und in Schweden angestrebte Erlangung einer „Herdenimmunität“ mittels einer hohen Zahl von Infektionen, unter der Maßgabe, dass es dabei zu keiner Überlastung des Gesundheitssystems kommt. Aufgrund des relativ hohen Sterberisikos hat diese Idee verständlicherweise wenig Zustimmung gefunden. Aber wie wäre es im günstigen Fall einer lang anhaltenden Immunität um die zeitliche Perspektive bestellt? Nimmt man als Belastungsgrenze die bislang maximal erreichte Zahl von täglichen Neuinfektionen in Deutschland an – fast 7.000 Neuinfektionen (27. März 2020) –, würde es rund 32 Jahre dauern, bis sich alle aktuell 83 Millionen Einwohner Deutschlands infiziert hätten. Berücksichtigt man eine in wissenschaftlichen Studien ermittelte Dunkelziffer von zwei bis zehn für das Verhältnis von tatsächlichen und erkannten Infektionen, ergibt sich immerhin noch ein Zeitraum von drei bis 16 Jahren. Dies ist zu vergleichen mit den geschätzten ein bis zwei Jahren bis zur Verfügbarkeit von Impfstoffen und der für die Impfung der Bevölkerung notwendigen Zeit. Eine genauere Berechnung müsste verschiedene weitere Aspekte berücksichtigen, u. a. die folgenden: eine verlangsamte Ausbreitung der Krankheit mit zunehmender Zahl von Infektionen, die Veränderung der Population durch Geburten und die Dauer einer Immunität nach überstandener Infektion.
Überlastung des Gesundheitssystems?
Wie nah das Gesundheitssystem tatsächlich vor einer Überlastung stand, lässt sich mit einer anderen Rechnung auf der Basis von Zahlen untersuchen, die natürlich erst im Laufe der Zeit verfügbar geworden sind: Das Verhältnis von im Zusammenhang mit COVID-19 verstorbenen zu infizierten Personen beträgt in Deutschland ca. 3 Prozent, das der intensivmedizinisch behandelten Personen zur Zahl der dabei Verstorbenen 4:1 (von den künstlich beatmeten Corona-Patienten sind in Deutschland sogar rund 50 Prozent verstorben), die mittlere Verweildauer in der Intensivstation zehn Tage und die Gesamtzahl der freien Intensivbetten 10.000 (Stand aller Angaben: Ende Juli 2020; Quellen: RKI, de.statista.com). Eine unmittelbare Schlussfolgerung ist, dass 12 Prozent aller Infizierten auf einer Intensivstation behandelt werden. Daraus folgt, dass sich Deutschland rund 8.000 Neuinfektionen pro Tag (100/12 ⨯ 10.000/10) „leisten“ könnte und sogar nur 4.000, wenn die Hälfte der Reservebetten für eine plötzliche Häufung anderer Notfälle reserviert bleiben soll. Für eine genauere Rechnung könnte die Abnahme des Durchschnittsalters der Infizierten seit dem Frühjahr berücksichtigt werden: Da es bei jüngeren Menschen tendenziell weniger schwere Verläufe gibt, würden sich die Werte vergrößern. Gemessen an dem Ziel, einer Überlastung des Gesundheitssystems vorzubeugen, hat die Politik im Frühjahr also noch zur rechten Zeit „die Notbremse gezogen“ – begleitet von hier nicht betrachteten Nebenwirkungen (die schnelle Abnahme der Neuinfektionen geht evtl. auch auf individuelle Vorsichtsmaßnahmen kurz vor dem Lockdown zurück).
Superspreading-Ereignisse
Beim Schulbetrieb in der Corona-Krise besteht die Sorge, dass Unterricht in Klassenräumen mit regulärer Belegung zu Superspreading- Ereignissen führt. Mit elementarer Wahrscheinlichkeitsrechnung lässt sich das Risiko dafür abschätzen. Wenn es sich als unzumutbar hoch herausstellen sollte, muss nicht zwangsläufig auf Unterricht im Klassenverband verzichtet werden, wenn ein geeignetes Hygienekonzept besteht. Eine der ersten Maßnahmen, die gegen Corona ergriffen und am längsten aufrechterhalten wurden, war in vielen Ländern das Verbot von Großveranstaltungen, weil diese dem Virus durch die physische Nähe vieler Menschen gute Verbreitungsmöglichkeiten bieten. Aber auch die Ansammlung weniger Menschen, z. B. von nur zweien, wurde zeitweilig untersagt. Die sich mit zunehmender Dauer eines Lockdowns bemerkbar machenden Nebenwirkungen führten zu Diskussionen über Lockerungen der beschlossenen Regelungen. Eine Ansammlung von Personen, die sich ohne effektiven Mund-Nasen- Schutz so nah kommen, dass es zwischen ihnen zu einer Ansteckung kommen kann (z. B. in Klassenräumen, Aufzügen, Bussen, Flugzeugen oder auf Partys), soll hier als „Gruppe“ verstanden werden.
Modelle zur Festlegung der Gruppengrößen
Für die Festlegung einer noch akzeptablen Gruppengröße sind selbst stark vereinfachte Modelle eine Alternative zur Entscheidung nach Bauchgefühl. Eine Größe, die sich exakt berechnen lässt, ist die Wahrscheinlichkeit, dass sich unter n Personen mindestens eine infizierte Person befindet. Dafür verwendet man der Einfachheit halber die Gegenwahrscheinlichkeit, dass alle Personen nicht infiziert („gesund“) sind. Wenn p die Wahrscheinlichkeit bezeichnet, dass eine Person infiziert ist, dann beträgt die Wahrscheinlichkeit, dass alle gesund sind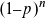 
. Dies gilt, sofern alle Infektionen (stochastisch) unabhängig voneinander sind, was z. B. bei Ehepaaren nicht erfüllt ist. Die Wahrscheinlichkeit, dass nicht alle gesund sind, dass es also mindestens einen Infizierten gibt, beträgt dann 1–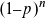. Es wurden zwei interaktive GeoGebra-Arbeitsblätter erstellt, mit denen sich diese Wahrscheinlichkeit für einen festen Wert von n bzw. ein Intervall von n berechnen lässt. Eingabeparameter sind die Größe der Population, z. B. die Einwohnerzahl von Deutschland, die Gesamtzahl der Infizierten, die Zahl der Genesenen und der Verstorbenen. Aus den letzten drei Parametern wird die Zahl der aktiven Fälle berechnet. Für kleine Werte von n (<100) und p (<10 Prozent) steigt die berechnete Wahrscheinlichkeit noch in guter Näherung linear. Im Unterricht könnte dies als Anwendungsfall für die Berechnung von Ableitungen und ggf. die Aufstellung von Taylorreihen betrachtet werden.
Wahrscheinlichkeitswerte als Entscheidungshilfen?
Die Berechnung von Wahrscheinlichkeitswerten kann eine Entscheidungshilfe sein, ersetzt aber keine Entscheidung. Für die Beurteilung von Wahrscheinlichkeiten sind Vergleiche nützlich, wie z. B.: Wie hoch ist die durchschnittliche Sterblichkeit in Deutschland (1.000 Todesfälle auf 100.000 Einwohner pro Jahr)? Welche Risiken ist die Gesellschaft in anderen Bereichen z. B. bereit zu akzeptieren? So betrug 2019 die Zahl der Verkehrstoten in Deutschland 3.059, was bei einer Einwohnerzahl von 83,02 Millionen einer Wahrscheinlichkeit von 1:27.000 entspricht. Dies macht deutlich, dass angewandte Mathematik, der die mathematische Beschreibung und Analyse einer Pandemie zugerechnet werden kann, neben dem eigentlichen Rechnen viele weitere Kompetenzen erfordert: u. a. Recherchieren, Modellieren und Argumentieren.
Prof. Dr. Daniel Gembris, Berufsakademie Sachsen, Staatliche Studienakademie Dresden
Download: Logarithmische Diagramme und Differentialgleichungen
Link-Tipps:
SARS-CoV-2-Steckbrief zur Coronavirus-Krankheit-2019 (COVID-19)
www.t1p.de/covid-steckbrief
Erfassung der SARS-CoV-2-Testzahlen in Deutschland
www.t1p.de/rki-testzahl
COVID-19-Karten der Johns Hopkins Universität
coronavirus.jhu.edu/map.html
Geogebra-Arbeitsblatt: Visualisierung der Wahrscheinlichkeit als Funktion der Gruppengröße
www.geogebra.org/m/b5yvxdmp
Ergänzung vom 01.02.2021:
Online-Simulation für die Bestimmung des Infektionsrisikos in Innenräumen (mit Visualisierung)
https://www.zeit.de/wissen/gesundheit/2020-11/coronavirus-aerosole-ansteckungsgefahr-infektion-hotspot-innenraeume
Simulation der TU Berlin: COVID-19 Infektionsrisiko durch Aerosole
https://hri-pira.github.io/
Eine regelmäßig aktualisierte Simulation des Infektionsgeschehens in Deutschland basierend auf dem SEIR-Modell von Professor Dr. Thorsten Lehr, Universität des Saarlandes
https://covid-simulator.com/
Daten zur Belegung der Intensivbetten in Deutschland
https://www.divi.de/divi-intensivregister-tagesreport-archiv
Simulator der TU Berlin für die Corona-Ausbreitung in Berlin
https://covid-sim.info/
Corona: Mathematik & Modellbildung
Unterichtmaterialien und Ideen zur mathematischen Modellierung der Coronapandemie
https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe2/mathematik-und-corona
